La cuantificación del tamaño del ventrículo derecho (VD) es crucial en determinadas cardiopatías congénitas. Para su evaluación se recomiendan distintas técnicas de imagen, siendo más accesible la medición de diámetros ventriculares mediante ecocardiografía. En pediatría la normalización de parámetros ecocardiográficos es compleja, escasa y heterogénea. El objetivo de este estudio consistió en establecer Z-score de diámetros de VD fiables y reproducibles capaces de predecir valores de referencia en población pediátrica sana española.
MétodosEstudio multicéntrico prospectivo de 661 pacientes sanos (edades 0-18 años, 43,5% mujeres). Los diámetros ecocardiográficos del VD se relacionaron con variables biométricas mediante distintas ecuaciones de regresión. Para su estandarización se analizaron factores de confusión (sexo, edad y variabilidad inter/intraobservador), heterocedasticidad y residuos (test Saphiro-Wilk y Breusch-Pagan).
ResultadosSe obtuvieron curvas de normalidad (Z-score) para cada diámetro del VD que permitieron predecir el valor medio de cada diámetro en función de la edad, peso, talla y distintas superficies corporales. La superficie corporal según fórmula de Haycock ofreció un excelente ajuste para los distintos diámetros basal, medial y longitudinal (R2 0,81; 0,82; 0,9). Los factores de confusión no aportaron cambios significativos, por lo que no fueron incluidos en los modelos finales (variabilidad inter- e intraobservador, CCI > 0,9).
ConclusionesSe brindan valores de referencia de diámetros VD de población pediátrica sana. Las curvas de Z-score ofrecidas cubren una importante carencia en cardiología pediátrica y son aplicables a todos los grupos de edad para evaluar el tamaño del VD, de gran interés clínico en la práctica diaria.
Right ventricle (RV) measurements are crucial for certain congenital heart diseases and various cardiovascular conditions. Echocardiographic RV diameters are especially useful for its assessment. Paediatric echocardiographic data standardisation in normal subjects is complex, scarce, and heterogeneous. The aim of this study was to establish reliable and reproducible echocardiographic reference values (Z-score) of RV diameters in a healthy Spanish paediatric cohort.
MethodsA multicentre study was conducted on 661 healthy subjects (age range 0-18 years, 43.5% female). Several regression models were tested to examine the relationship between RV diameters and biometric variables. Heteroscedasticity and residual associations (Shapiro-Wilk and Breusch-Pagan tests) and confounding factors (gender, age, inter/intraobserver agreement) were considered for an unbiased standardisation.
ResultsStructured Z-scores were computed for each RV diameter. Predicted mean value for each diameter was determined according to age, weight, height, and different body surface area. The Haycock formula provided the best fit for basal, midcavity, and longitudinal diameters (R2 0.81; 0.82; 0.9). Confounders were not significant, and therefore not included in final models (inter/intraobserver agreement > 0.9).
ConclusionsThis study reports reference values for echocardiographic RV diameters from a Spanish healthy paediatric cohort using a rigorous statistical design. These Z-scores partly cover a gap in current paediatric cardiology and represent a relevant diagnostic tool for clinical practice, as well as a useful guide to decision making at any paediatric stage.
En cardiología pediátrica muchas decisiones clínicas, intervencionistas o quirúrgicas se toman en función del tamaño de las estructuras cardiacas. El seguimiento de niños intervenidos o no de cardiopatías congénitas también depende de identificar cómo se desvía el crecimiento cardiaco del esperado. Para detectar cambios patológicos en la estructura cardiaca primero se debe definir con precisión qué es normal.
En pediatría el tamaño cardiaco normal varía en función de diversos determinantes biométricos inherentes al desarrollo del niño y se ve alterado por múltiples factores de confusión. Aunque recientemente se han publicado guías para el estudio del ventrículo derecho (VD) en adultos1 en la actualidad no existen guías para la evaluación ecocardiográfica del VD en pediatría, por ello el desarrollo de valores de referencia validados y fiables es de gran importancia2. Determinar el tamaño del VD normal en población pediátrica sana permitirá evaluar de forma óptima a pacientes con alteraciones, con implicaciones diagnósticas y pronósticas.
Este trabajo se centra en la medición de diámetros ventriculares derechos de niños sanos, obteniendo rangos de normalidad (Z-score) útiles para detectar VD anómalos de forma fácil y reproducible.
MétodosEstudio observacional, transversal, prospectivo, multicéntrico de 661 niños sanos reclutados durante 4 años en las consultas de Cardiología Pediátrica. El tamaño muestral necesario dentro de cada grupo etario para que fuese representativo de la población general se estimó en ≥ 88 pacientes. Dicho tamaño se calculó con un intervalo de confianza del 95%, un margen de error del 0,106 y estimando una desviación estándar de 0,5.
Los niños fueron clasificados en estratos de edad de acuerdo con los grupos etarios establecidos por la OMS: neonatos (0 a 28 días de vida), lactantes (29 días de vida a 24 meses) preescolares (25 meses a 5 años) escolares (6 a 10 años), adolescentes (11 a 18 años).
Criterios de inclusiónPacientes caucásicos sanos que acudían por soplo funcional u otros motivos sin presentar alteraciones electrocardiográficas ni ecocardiográficas congénitas o adquiridas. Se consideró normal un pequeño ductus arterioso sin repercusión durante los primeros 3 días de vida o un foramen oval permeable.
Criterios de exclusiónSe excluyeron pacientes con deformidad torácica, enfermedad neuromuscular, síndromes y crosomopatías, hipertensión arterial o hipertensión pulmonar, antecedentes familiares de enfermedad genética (ej. síndrome Marfan), edad ≥ 19 años y recién nacidos prematuros.
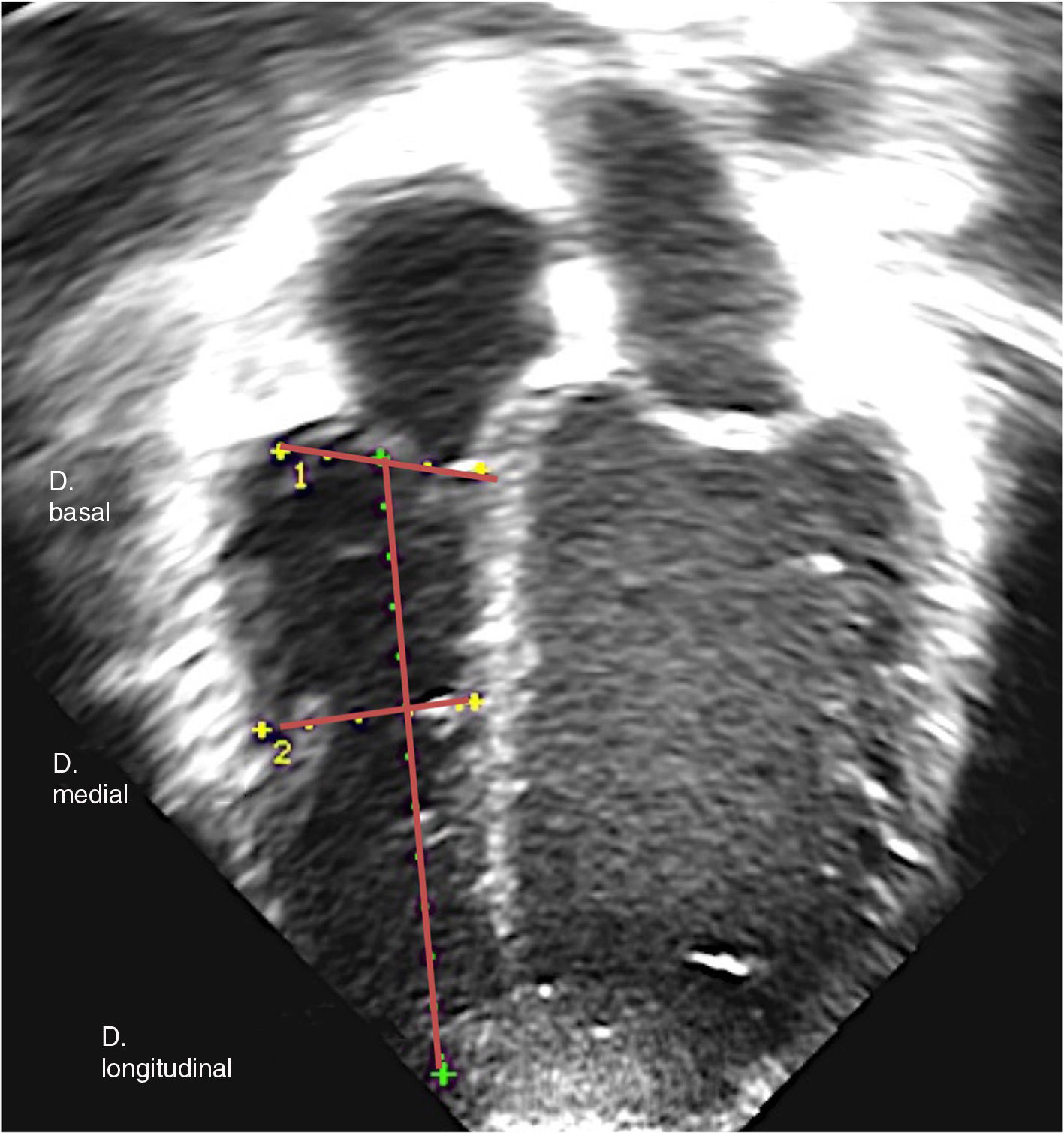
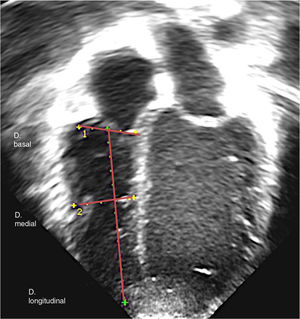
Examen ecocardiográficoSe emplearon dos ecocardiógrafos: Phillips iE33 (Phillips Medical Systems, Bothell, WA) e Hitachi Aloka Pro Sound Alpha 7 (Aloka Medical Ltd.). Se tomaron las imágenes con sondas multifrecuencia de 8MHz para neonatos y edades próximas y transductores de 5MHz a mayor edad y peso. Se registraron tres ciclos cardiacos y cada medida se calculó dos veces (en distintos latidos) extrayendo la media de ambos valores. Se determinaron los diámetros ventriculares basal, medial y longitudinal de forma estandarizada en plano apical de 4 cámaras siguiendo las guías de medición del VD3,4 (fig. 1) por tres ecocardiografistas expertos (variaciones interobservador descritas más adelante). Las imágenes se obtuvieron en telediástole (momento inmediatamente anterior al cierre de la válvula tricúspide, coincidiendo con el inicio del QRS) con registro ECG simultáneo e incluyendo las trabeculaciones (se midió hasta el borde endocárdico). El análisis se realizó indistintamente en el ecocardiógrafo o en la estación de trabajo posproceso Echopac versión 6.3.6 (GE Medical Systems). No se apreciaron diferencias significativas en cuanto al tipo de ecógrafo ni análisis posproceso. Solo fueron incluidos pacientes con buena ventana ecocardiográfica y buena calidad de imagen (visualización del endocardio y pared lateral del VD en su totalidad).
Definiciones y valores de referenciaConsideramos diámetros de VD normales a los comprendidos entre ± 2 Z-score. Se aplicaron fórmulas de superficie corporal de Haycock, DuBois, Mosteller, Boyd, Gehan y Meban para la normalización de diámetros VD5–10.
Análisis estadísticoLa estandarización de los distintos diámetros se obtuvo gracias a modelos de normalización paramétrica (Z-score) que se ajustaron según edad y variables biométricas (peso, talla y superficies corporales). Se probaron distintas ecuaciones de regresión (lineal, logarítmica, exponencial, raíz cuadrada y cúbica) capaces de relacionar los parámetros a estudio. Para todos los modelos se realizó un análisis de residuos mediante métodos gráficos y contrastes de hipótesis sobre normalidad (test de Saphiro-Wilk) y sobre homocedasticidad (test de Breusch-Pagan). Para todos los test se consideraron bilaterales y significativas las asociaciones estadísticas con valor de p < 0,05.
De los modelos que cumplían la hipótesis se seleccionó el más sencillo y con mejor ajuste (R2) para establecer las curvas de Z-score, valor estandarizado que indica cuántas desviaciones estándar por encima o por debajo de la media en una población normal se sitúa una medida determinada.
Se usaron modelos multivariantes y análisis estratificado para evaluar el efecto del sexo como factor de confusión. Veinte sujetos fueron sometidos a un estudio de concordancia inter- e intraobservador. El coeficiente de correlación intraclase (CCI) fue calculado mediante análisis de la varianza de medidas repetidas con modelos mixtos.
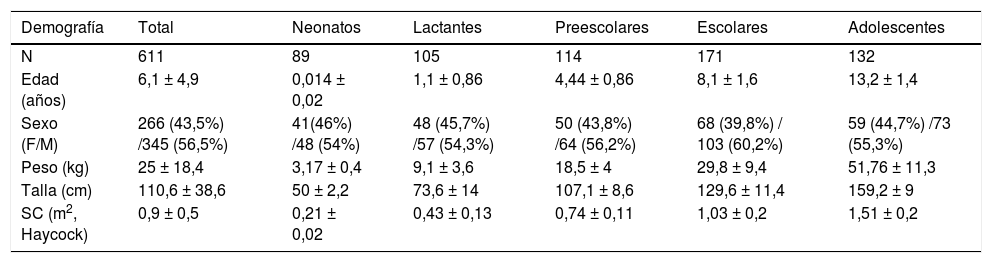
ResultadosDescripción de la muestraLas características demográficas se muestran en la tabla 1. La distribución de los diámetros ventriculares derechos por grupos de edad se presenta en la tabla 2.
Datos demográficos de la muestra expresados como media ± DE (rango) o como número (porcentaje)
| Demografía | Total | Neonatos | Lactantes | Preescolares | Escolares | Adolescentes |
|---|---|---|---|---|---|---|
| N | 611 | 89 | 105 | 114 | 171 | 132 |
| Edad (años) | 6,1 ± 4,9 | 0,014 ± 0,02 | 1,1 ± 0,86 | 4,44 ± 0,86 | 8,1 ± 1,6 | 13,2 ± 1,4 |
| Sexo (F/M) | 266 (43,5%) /345 (56,5%) | 41(46%) /48 (54%) | 48 (45,7%) /57 (54,3%) | 50 (43,8%) /64 (56,2%) | 68 (39,8%) / 103 (60,2%) | 59 (44,7%) /73 (55,3%) |
| Peso (kg) | 25 ± 18,4 | 3,17 ± 0,4 | 9,1 ± 3,6 | 18,5 ± 4 | 29,8 ± 9,4 | 51,76 ± 11,3 |
| Talla (cm) | 110,6 ± 38,6 | 50 ± 2,2 | 73,6 ± 14 | 107,1 ± 8,6 | 129,6 ± 11,4 | 159,2 ± 9 |
| SC (m2, Haycock) | 0,9 ± 0,5 | 0,21 ± 0,02 | 0,43 ± 0,13 | 0,74 ± 0,11 | 1,03 ± 0,2 | 1,51 ± 0,2 |
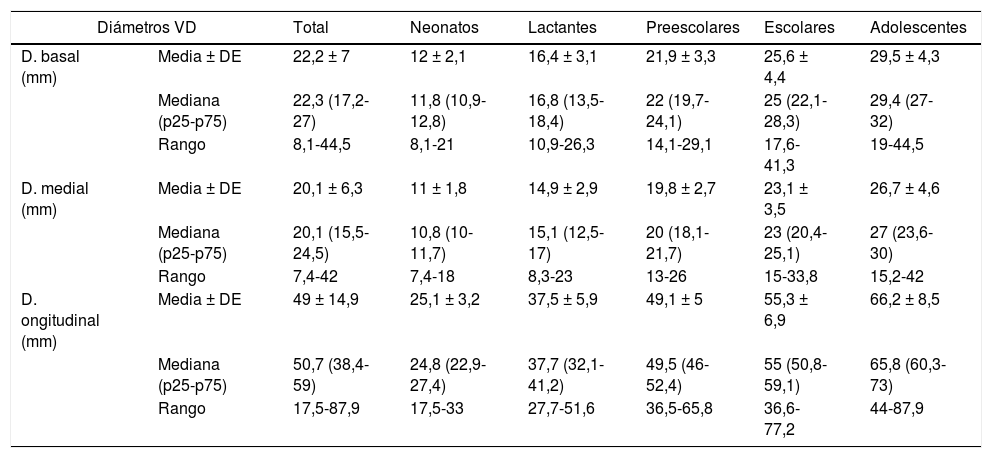
Distribución de los diámetros ventriculares derechos por grupos de edad
| Diámetros VD | Total | Neonatos | Lactantes | Preescolares | Escolares | Adolescentes | |
|---|---|---|---|---|---|---|---|
| D. basal (mm) | Media ± DE | 22,2 ± 7 | 12 ± 2,1 | 16,4 ± 3,1 | 21,9 ± 3,3 | 25,6 ± 4,4 | 29,5 ± 4,3 |
| Mediana (p25-p75) | 22,3 (17,2-27) | 11,8 (10,9-12,8) | 16,8 (13,5-18,4) | 22 (19,7-24,1) | 25 (22,1-28,3) | 29,4 (27-32) | |
| Rango | 8,1-44,5 | 8,1-21 | 10,9-26,3 | 14,1-29,1 | 17,6-41,3 | 19-44,5 | |
| D. medial (mm) | Media ± DE | 20,1 ± 6,3 | 11 ± 1,8 | 14,9 ± 2,9 | 19,8 ± 2,7 | 23,1 ± 3,5 | 26,7 ± 4,6 |
| Mediana (p25-p75) | 20,1 (15,5-24,5) | 10,8 (10-11,7) | 15,1 (12,5-17) | 20 (18,1-21,7) | 23 (20,4-25,1) | 27 (23,6-30) | |
| Rango | 7,4-42 | 7,4-18 | 8,3-23 | 13-26 | 15-33,8 | 15,2-42 | |
| D. ongitudinal (mm) | Media ± DE | 49 ± 14,9 | 25,1 ± 3,2 | 37,5 ± 5,9 | 49,1 ± 5 | 55,3 ± 6,9 | 66,2 ± 8,5 |
| Mediana (p25-p75) | 50,7 (38,4-59) | 24,8 (22,9-27,4) | 37,7 (32,1-41,2) | 49,5 (46-52,4) | 55 (50,8-59,1) | 65,8 (60,3-73) | |
| Rango | 17,5-87,9 | 17,5-33 | 27,7-51,6 | 36,5-65,8 | 36,6-77,2 | 44-87,9 | |
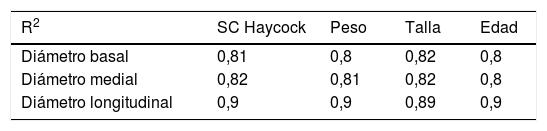
De los modelos que cumplieron los supuestos de normalidad de residuos y homocedasticidad se seleccionó el que ofreció mayor coeficiente de determinación, encontrando diferencias mínimas entre los distintos parámetros biométricos y superficies corporales (tabla 3). Se eligió como mejor parámetro biométrico para normalizar diámetros del VD la superficie corporal según fórmula de Haycock1,4,11,12 (R2 0,81; 0,82; 0,9 para los distintos diámetros), seguido de peso, talla y finalmente la edad.
Las ecuaciones de regresión que ofrecieron un mejor ajuste entre los distintos diámetros y la SC fueron las no lineales.
Para relacionar el diámetro basal y superficie corporal según fórmula de Haycock se empleó la transformación de variables en ecuaciones de raíz cuadrada:
ln(y) = A + B x √(x), calculando Z = (ln[medida] – [A + B x √SC]) / √EEM
Para los diámetros medial y longitudinal las ecuaciones exponenciales fueron las más precisas:
ln(y) = A + B x ln(x), calculando Z = (ln[medida] – [A + B x ln(SC]) / √EEM
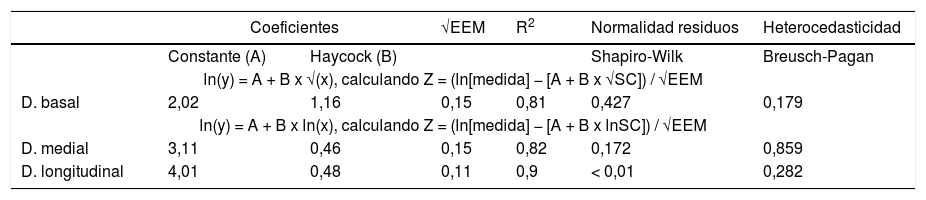
Estas ecuaciones satisficieron la asunción de homocedasticidad y normalidad de los residuos, mostrando R2 óptimos (tabla 4), permitiendo mantener una varianza más estable y constante a lo largo del rango completo del tamaño corporal.
Ecuaciones de regresión que relacionan los diámetros ventriculares derechos con la superficie corporal (SC) según fórmula de Haycock. Test de normalidad Saphiro-Wilk. Test de homocedasticidad Breusch-Pagan. Error estándar de la media (EEM). Coeficiente de determinación (R2)
| Coeficientes | √EEM | R2 | Normalidad residuos | Heterocedasticidad | ||
|---|---|---|---|---|---|---|
| Constante (A) | Haycock (B) | Shapiro-Wilk | Breusch-Pagan | |||
| ln(y) = A + B x √(x), calculando Z = (ln[medida] − [A + B x √SC]) / √EEM | ||||||
| D. basal | 2,02 | 1,16 | 0,15 | 0,81 | 0,427 | 0,179 |
| ln(y) = A + B x ln(x), calculando Z = (ln[medida] − [A + B x lnSC]) / √EEM | ||||||
| D. medial | 3,11 | 0,46 | 0,15 | 0,82 | 0,172 | 0,859 |
| D. longitudinal | 4,01 | 0,48 | 0,11 | 0,9 | < 0,01 | 0,282 |
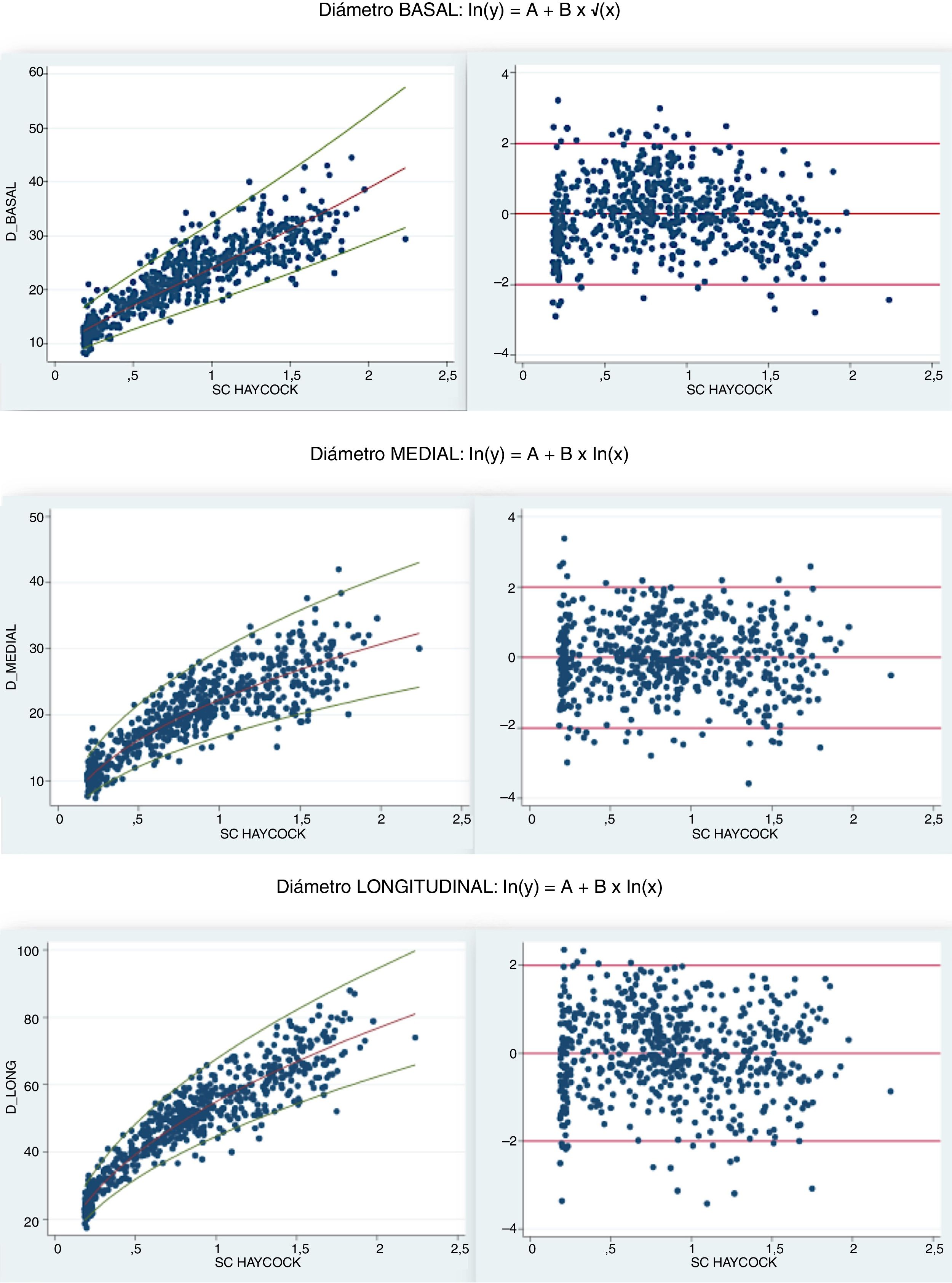
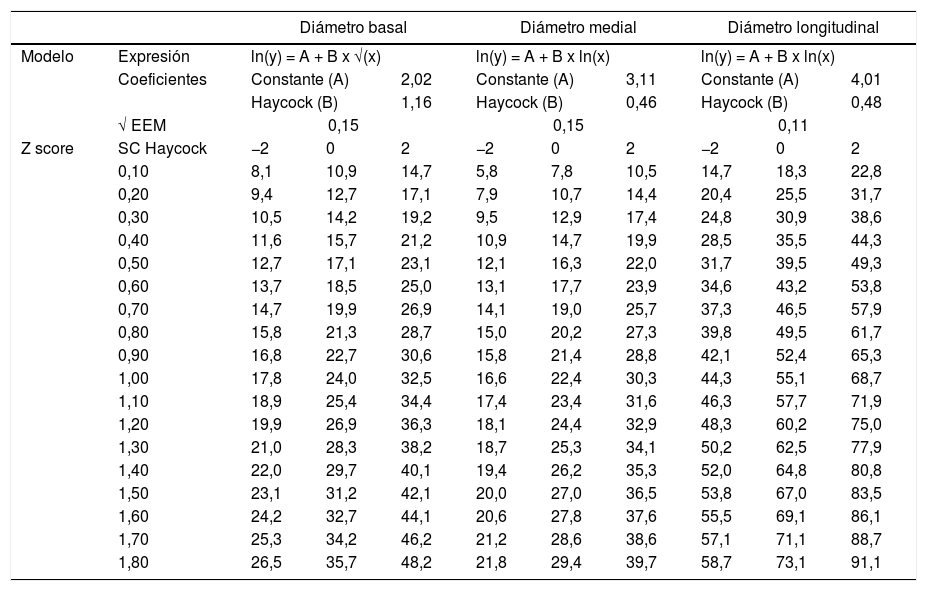
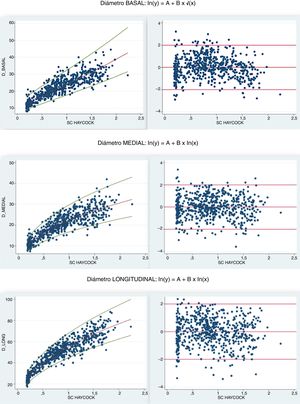
A continuación se muestran las gráficas de Z-score para los distintos diámetros ventriculares derechos en función de SC (fórmula de Haycock), junto con sus modelos de regresión, residuos estandarizados y homocedasticidad (fig. 2). Se puede estimar el Z-score de los diámetros VD localizando el valor en las curvas de Z-score o bien en la tabla 5.
Z-score de 0 y ± 2 de diámetros VD normalizados por superficie corporal (SC) según fórmula de Haycock
| Diámetro basal | Diámetro medial | Diámetro longitudinal | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Modelo | Expresión | ln(y) = A + B x √(x) | ln(y) = A + B x ln(x) | ln(y) = A + B x ln(x) | ||||||
| Coeficientes | Constante (A) | 2,02 | Constante (A) | 3,11 | Constante (A) | 4,01 | ||||
| Haycock (B) | 1,16 | Haycock (B) | 0,46 | Haycock (B) | 0,48 | |||||
| √ EEM | 0,15 | 0,15 | 0,11 | |||||||
| Z score | SC Haycock | −2 | 0 | 2 | −2 | 0 | 2 | −2 | 0 | 2 |
| 0,10 | 8,1 | 10,9 | 14,7 | 5,8 | 7,8 | 10,5 | 14,7 | 18,3 | 22,8 | |
| 0,20 | 9,4 | 12,7 | 17,1 | 7,9 | 10,7 | 14,4 | 20,4 | 25,5 | 31,7 | |
| 0,30 | 10,5 | 14,2 | 19,2 | 9,5 | 12,9 | 17,4 | 24,8 | 30,9 | 38,6 | |
| 0,40 | 11,6 | 15,7 | 21,2 | 10,9 | 14,7 | 19,9 | 28,5 | 35,5 | 44,3 | |
| 0,50 | 12,7 | 17,1 | 23,1 | 12,1 | 16,3 | 22,0 | 31,7 | 39,5 | 49,3 | |
| 0,60 | 13,7 | 18,5 | 25,0 | 13,1 | 17,7 | 23,9 | 34,6 | 43,2 | 53,8 | |
| 0,70 | 14,7 | 19,9 | 26,9 | 14,1 | 19,0 | 25,7 | 37,3 | 46,5 | 57,9 | |
| 0,80 | 15,8 | 21,3 | 28,7 | 15,0 | 20,2 | 27,3 | 39,8 | 49,5 | 61,7 | |
| 0,90 | 16,8 | 22,7 | 30,6 | 15,8 | 21,4 | 28,8 | 42,1 | 52,4 | 65,3 | |
| 1,00 | 17,8 | 24,0 | 32,5 | 16,6 | 22,4 | 30,3 | 44,3 | 55,1 | 68,7 | |
| 1,10 | 18,9 | 25,4 | 34,4 | 17,4 | 23,4 | 31,6 | 46,3 | 57,7 | 71,9 | |
| 1,20 | 19,9 | 26,9 | 36,3 | 18,1 | 24,4 | 32,9 | 48,3 | 60,2 | 75,0 | |
| 1,30 | 21,0 | 28,3 | 38,2 | 18,7 | 25,3 | 34,1 | 50,2 | 62,5 | 77,9 | |
| 1,40 | 22,0 | 29,7 | 40,1 | 19,4 | 26,2 | 35,3 | 52,0 | 64,8 | 80,8 | |
| 1,50 | 23,1 | 31,2 | 42,1 | 20,0 | 27,0 | 36,5 | 53,8 | 67,0 | 83,5 | |
| 1,60 | 24,2 | 32,7 | 44,1 | 20,6 | 27,8 | 37,6 | 55,5 | 69,1 | 86,1 | |
| 1,70 | 25,3 | 34,2 | 46,2 | 21,2 | 28,6 | 38,6 | 57,1 | 71,1 | 88,7 | |
| 1,80 | 26,5 | 35,7 | 48,2 | 21,8 | 29,4 | 39,7 | 58,7 | 73,1 | 91,1 | |
Se ajustaron modelos multivariantes añadiendo el sexo como factor de confusión. Se apreció un efecto estadísticamente significativo (p < 0,05), pero despreciable. Posteriormente se realizó un análisis por estratos de edad añadiendo la variable sexo. Objetivamos estimaciones prácticamente iguales, por lo que se desestimó ajustar los distintos modelos según el género.
Se analizó la influencia de la edad sobre los distintos diámetros ventriculares, encontrando valores elevados de R2 (0,79; 0,8; 0,9) que tradujeron una fuerte asociación entre ambas variables.
En el grupo neonatal se investigó la relación entre los diámetros ventriculares y el peso. El mejor R2 fue del 5,7% sin cumplir la hipótesis de normalidad de residuos. Se analizó también la relación entre los diámetros ventriculares y la fórmula de Meban. Al aplicar distintos modelos para establecer la asociación, encontramos que el mejor coeficiente de determinación fue del 4%, sin cumplir la hipótesis de normalidad de residuos.
En el grupo de adolescentes se estudió la relación entre diámetros ventriculares y talla. El mejor modelo verificando las hipótesis obtuvo un R2 del 14%.
Variabilidad inter- e intraobservadorFue evaluada en 20 pacientes con muy buena concordancia (CCI > 0,9) para todas las medidas. El diámetro medial fue el que presentó mayor variabilidad interobservador.
Comparación con la literaturaSe ofrecen curvas de Z-score basadas en población caucásica española sana. Existen otros autores que también han realizado curvas de Z-score en pediatría. Consideramos muy interesante comparar las curvas de Z-score propuestas con las descritas por Koestenberger13 y Cantinotti11 de forma gráfica y calculando el índice de concordancia.
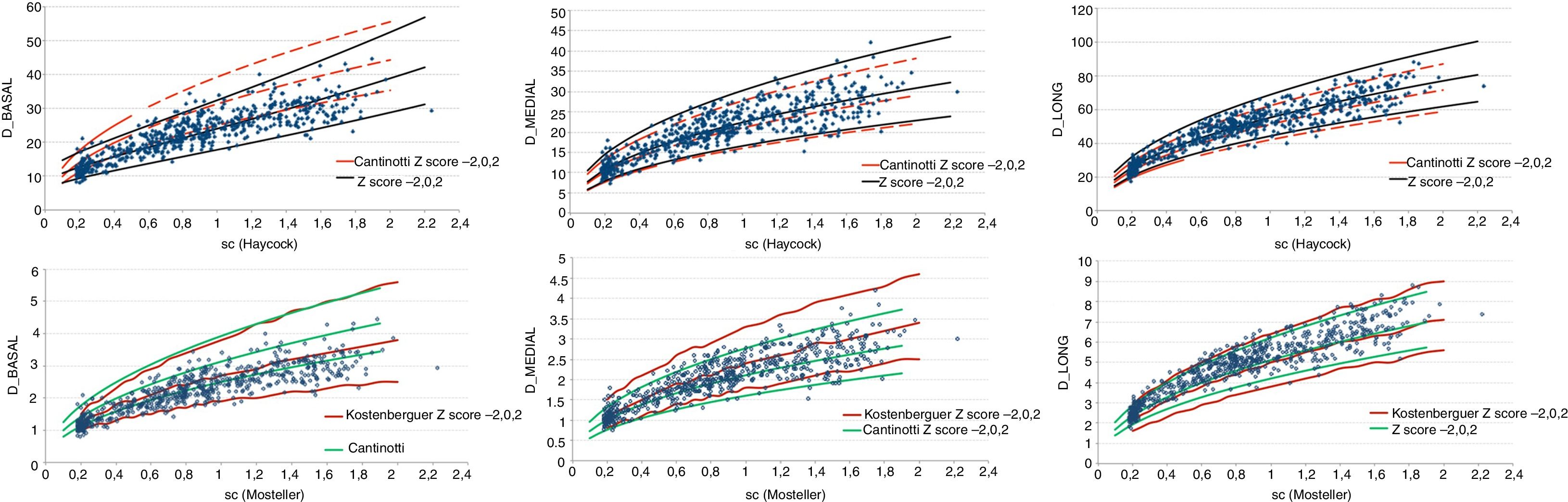
Cantinotti normalizó valores según la fórmula de SC de Haycock, ofreciendo sus modelos de regresión. Se muestran a continuación las gráficas que enfrentan nuestras curvas de Z-score con las de este autor (fig. 3). Se halló buena concordancia para los diámetros medial y longitudinal (índices de concordancia de 0,9 y 0,76) e infraestimación para el diámetro basal (índice de concordancia 0,36).
Koestenberger normalizó diámetros del VD según la fórmula de superficie corporal de Mosteller y según la edad. En su artículo no describió los modelos de regresión empleados, por lo que no se pudieron calcular índices de concordancia. Enfrentando los valores de Z-score de este trabajo frente a los descritos por Koestenberger de forma gráfica se descubrió mayor concordancia subjetiva con los diámetros medial y longitudinal, infraestimando de nuevo el Z-score del diámetro basal.
Ante la desigualdad obtenida para el diámetro basal, comparamos ambos autores entre ellos, normalizando los diámetros VD por SC. Se objetivó buena correlación de nuevo para los diámetros medial y longitudinal y discrepancia para el diámetro basal.
DiscusiónEl estudio del tamaño VD por imagen es esencial ya que muchas decisiones clínicas y quirúrgicas en cardiología pediátrica se toman en función de las medidas de esta cavidad. Nuestro trabajo plantea el abordaje mediante ecocardiografía 2D por tratarse de una técnica sencilla, económica y ampliamente accesible. Los diámetros del VD en la porción de entrada y trabeculada constituyen una medida óptima por su reproducibilidad, facilidad de obtención en plano apical 4 cámaras y una amplia evidencia que los avala. No obstante, no debemos olvidar la porción de salida del VD, significativamente dilatada en ciertas cardiopatías congénitas.
La necesidad de normalizar parámetros ecocardiográficos en cardiología pediátrica surge de algo tan obvio como establecer valores de referencia. Una vez se conozca y se describa lo que es normal se podrá detectar lo que es patológico. A pesar de estas necesidades, reflejadas en las principales guías ecocardiográficas4,14, el esfuerzo por estandarizar medidas cardiacas en población pediátrica todavía no ha culminado. Se han propuesto rangos de referencia para la mayoría de las estructuras cardiacas15, pero no existen guías específicas para la evaluación del VD en pediatría y las guías disponibles para la valoración del VD en adultos2,3 no son aplicables a niños porque no ajustan sus medidas con parámetros biométricos (superficie corporal).
Diversos autores12 han demostrado que, a pesar de los avances metodológicos, la normalización de medidas ecocardiográficas en pediatría no está correctamente validada y que por tanto no es fiable11,13.
Este estudio cumple los requisitos inherentes a la normalización de medidas ecocardiográficas descritos en la literatura12,16,17 por varios motivos:
- 1.
Los diámetros VD se han recogido de forma estandarizada siguiendo las guías de recomendación.
- 2.
La cohorte estudiada fue homogénea en cuanto a tamaño muestral por grupo etario y etnia (caucásica), lo que hace posible extraer valores normales para una población específica (española en particular, caucásica en general) y compararla con poblaciones de las mismas características y distintas razas.
- 3.
Se ha elegido el mejor parámetro biométrico para la normalización de diámetros ventriculares derechos (SC por fórmula de Haycock), seguido de peso, talla y edad.
Normalizar parámetros ecocardiográficos en pediatría es difícil por la alometría (influencia del crecimiento corporal sobre las cavidades cardiacas) y otros factores de confusión. Esta situación acarrea alta variabilidad y discordancia para una misma medida, con repercusión en las decisiones clínicas. Para resolver este problema las medidas ecocardiográficas se ajustan en función de variables biométricas (peso, talla o superficie corporal) porque así se puede evaluar el cambio de las dimensiones cardiacas en el niño que crece. Sin embargo, todavía existe controversia sobre cuál es el mejor parámetro biométrico. Diversos autores sugieren que, en general, la superficie corporal es mejor indicador de crecimiento somático que el peso o la talla de forma aislada en pediatría1,18. En nuestro caso, la mejor asociación fue también con la superficie corporal (aunque seguida muy de cerca por el peso) y una menor dependencia de talla y edad.
La SC no es un parámetro perfecto, ya que dependiendo de la fórmula empleada se obtendrán distintos valores normalizados para una misma medida, con mayor variabilidad cuanto mayor o menor peso o talla tenga el paciente. Ante esta situación, en nuestro trabajo se buscaron diferencias entre las distintas fórmulas de SC, encontrando R2 > 0,99 entre ellas, lo que sugiere que se podría usar cualquier fórmula de SC para normalizar diámetros VD.
- 4.
Ninguna variable siguió una distribución normal, asociando heterocedasticidad y residuos. Para contrarrestar estos fenómenos, se emplearon métodos estadísticos específicos15-17 y se aplicaron métodos paramétricos: construcción de gráficas de Z-score que relacionan los diámetros del VD (variable dependiente) con la superficie corporal (variable independiente) mediante ecuaciones de regresión capaces de predecir la media teórica del diámetro VD para una determinada superficie corporal.
Usar Z-score en pediatría es esencial porque estima la distribución de los valores de medición a través del rango de tamaño corporal en la población normal y aportan la magnitud de la anormalidad. Su uso está avalado y recomendado por las Guías Americanas de Ecocardiografía como el mejor método de normalización paramétrica para establecer valores de referencia. No obstante, no suponen verdades absolutas y se deben encajar siempre en el contexto clínico del paciente19.
- 5.
Se estudiaron modelos de regresión lineales y no lineales. Se eligieron modelos no lineales (exponenciales y de raíz cuadrada) por ser más sencillos y por ajustar las variables correctamente de forma estadística y visual a toda la muestra.
Para evitar la heterocedasticidad y lograr resultados extrapolables a la población general se emplearon logaritmos y raíz cuadrada de las variables en las fórmulas de regresión y se aplicó el test de Breusch-Pagan. El test de Saphiro-Wilk permitió seleccionar los modelos con normalidad de residuos que cumplían la premisa de que su alto poder explicativo también fuese bueno para predecir.
- 6.
Se analizaron factores de confusión sin alterar los resultados de forma significativa.
Los factores de confusión aplicados a nuestra muestra fueron edad, sexo y variabilidad inter- e intraobservador. Se emplearon modelos multivariantes y de análisis de la varianza para evaluar el efecto de estos factores de confusión sobre los diámetros ventriculares.
En nuestro trabajo la asociación de la edad con los diámetros VD presentó valores de R2 elevados, muy próximos a los alcanzados con la SC, indicando una fuerte asociación entre ambas variables. Existe evidencia de que los grupos etarios extremos (neonatos y adolescentes) requieren un estudio independiente. En ellos, el uso de la SC es más controvertido. Ahn et al.20-22 defienden que el peso se ajusta mejor en neonatos y Motz et al.23,24 abogan por la talla en adolescentes, por lo que se establecieron ambas asociaciones. Se objetivó que los coeficientes de determinación fueron significativamente menores sin cumplir la hipótesis de normalidad de residuos. La discrepancia de nuestros hallazgos posiblemente se explique porque los artículos mencionados analizan variables distintas.
Encontramos un efecto significativo del sexo, pero a la vez despreciable, por lo que no se incluyó en los modelos finales. Multitud de artículos avalan la influencia del sexo sobre las medidas cardiacas en adultos25-27, mientras que en pediatría Cantinotti describe unos resultados similares a los nuestros1,11,12. Es posible que el sexo se vuelva relevante a mayor edad28, lo que explicaría que los resultados pediátricos y de adultos sean diferentes.
Por último, el análisis de la variabilidad inter- e intraobservador mostró un CCI alto (0,89-0,98) lo que avala la reproducibilidad del estudio.
- 7.
Se han comparado las curvas de Z-score realizadas con las ofrecidas en la literatura.
Nuestros resultados revelan buena concordancia con los valores propuestos por Koestenberger13 y Cantinotti12 para los diámetros medial y longitudinal normalizados por SC, no así para el diámetro basal. Ante estas discordancias se comparó a ambos autores entre sí apreciando buena correlación de nuevo para los diámetros medial y longitudinal y discrepancia para el basal. Quizás merezca la pena reflexionar sobre si el mejor parámetro para normalizar el diámetro basal podría ser la edad (u otro distinto a la superficie corporal) o considerar que existan factores dependientes de la medición de este diámetro que interfieran con su estimación, como por ejemplo la variabilidad del diámetro basal asociada al plano apical de 4 cámaras. Por otro lado, el hecho de que existan discrepancias entre los Z-score apoya la decisión de realizar medidas de normalización propias.
ConclusionesGracias a una muestra representativa y una robusta estadística y sistemática en la obtención de imágenes se han realizado curvas de Z-score de diámetros ventriculares fiables y reproducibles.
Se establecen valores de referencia, escasos en la literatura actual, que aportan exactitud y precisión a las medidas ecocardiográficas del VD, de gran utilidad en la práctica clínica.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Al conjunto de autores. Sin su ayuda y orientación mi tesis y este trabajo no hubieran sido posibles.