Editado por: Paz González Rodríguez
Madrid Health Service. Primary Care Paediatrics. Madrid . España
María Aparicio Rodrigo
Madrid Health Service. Primary Care Paediatrics. Complutense University of Madrid. Madrid . España
Última actualización: Octubre 2025
Más datosLos resultados de los estudios epidemiológicos deben ser expresados en forma de medidas de salud o enfermedad. En este artículo repasamos las principales medidas de frecuencia, riesgo e impacto, que se pueden estimar usando, según el caso, proporciones, cocientes o tasas. Veremos que a cada estudio, en función de su diseño, le corresponden diferentes medidas. En un estudio transversal estimaremos la prevalencia; en un estudio de cohortes la incidencia, el riesgo relativo y las fracciones atribuibles; en un estudio de casos y controles la odds ratio; en un ensayo clínico el riesgo relativo, las reducciones absoluta y relativa del riesgo y el número necesario a tratar. Presentaremos los criterios de interpretación de todas estas medidas con ejemplos concretos.
The results of epidemiological studies should be expressed in terms of measures of health or disease. This article reviews the key frequency, risk and impact measures, which can be estimated using proportions, ratios or rates, depending on the specific context. It discusses which measures are appropriate for a study based on its design. Cross-sectional studies serve to estimate the prevalence; cohort studies allow calculation of the incidence, relative risk and attributable fractions; case-control studies use the odds ratio and clinical trials determine the relative risk, absolute and relative risk reductions and number needed to treat (NNT). The article also outlines criteria for the interpretation of these measures, supported by specific examples.
Los resultados de los estudios epidemiológicos deben ser expresados en forma de medidas de salud o enfermedad, con las que indicamos frecuencias, diferencias, asociación, riesgo o impacto. La forma de presentar los resultados va a depender del tipo de estudio realizado, pero, sobre todo, de las características de la variable o variables de interés. En función del tipo o tipos de variables implicados podremos recurrir a distintas medidas epidemiológicas.
En epidemiología, el escenario más simple lo constituye el estudio de 2variables discretas dicotómicas. Este escenario corresponde al supuesto habitual de estudio de la asociación entre presencia-ausencia de un determinado factor de exposición y presencia-ausencia de enfermedad. Para analizar esta relación contamos con una serie de medidas de frecuencia, riesgo e impacto.
Las medidas de frecuencia describen la distribución de la enfermedad en la población y su utilidad es describir la enfermedad, sería el primer paso de la investigación. Las medidas de asociación son útiles para conocer cómo se relaciona la enfermedad con los factores de riesgo, su magnitud e importancia. Las medidas de impacto son útiles para estimar la potencial repercusión de medidas de prevención o tratamiento.
Otro escenario habitual es el que evalúa la asociación entre una variable discreta y otra continua. Este escenario corresponde a estudios que evalúan la repercusión de un factor de exposición (p. ej., tratamiento versus placebo) sobre un efecto cuantificable en un rango continuo de valores (por ejemplo: presión arterial); en estos estudios la presentación de resultados se basará en las diferencias de medidas de tendencia (media, mediana) y dispersión de la variable continua entre grupos.
Conceptos previosEmpezaremos repasando algunos conceptos aritméticos en los que se basan las medidas epidemiológicas: la proporción, el cociente y la tasa1.
Una proporción es un número de observaciones con una característica dada (por ejemplo, neonatos con malformaciones congénitas) dividido por el total de observaciones, con y sin dicha característica, en un grupo determinado (por ejemplo, todos los recién nacidos en un periodo con o sin malformación). En las proporciones el numerador está incluido en el denominador. El resultado se expresa con cifras decimales ente 0 y 1 y equivale a la probabilidad de la característica evaluada (en porcentajes, entre 0 y 100).
Un cociente o razón es la división entre 2números cualesquiera, en la que el numerador no está incluido en el denominador. Por ejemplo, el índice de masa corporal, que es el cociente entre el peso en kilogramos y la talla en metros al cuadrado.
Una tasa se define genéricamente como el cambio de la magnitud de un parámetro por unidad del cambio de otro. Es, por tanto, una medida dinámica, que nos permite medir no solo la probabilidad de la característica evaluada, sino la velocidad con la que aparece. Por ejemplo, se expresa como tasa el número de recaídas de una enfermedad en función del tiempo de seguimiento de cada paciente.
Una odds es un término anglosajón que tiene una mala traducción en español (razón de posibilidades, razón de ventajas), por lo que lo hemos adoptado como tal. Es el cociente entre la probabilidad que ocurra un suceso (P) dividido por la probabilidad de que no ocurra (1-P).
Medidas de frecuenciaIncidencia y prevalencia son las expresiones de frecuencia de enfermedad más utilizadas en la literatura médica1,2. Es importante distinguirlas.
La prevalencia es el número de individuos con una enfermedad o característica en un determinado punto en el tiempo, dividido por la población en riesgo en ese momento. Si medimos los casos que existirían en cualquier momento durante un período específico de tiempo hablaremos de prevalencia de periodo. Se calcula habitualmente a partir de estudios transversales y se expresa como una proporción. Por ejemplo, si hay 250 niños con obesidad entre un total de 1.000 atendidos en un centro de salud, la prevalencia de obesidad es 0,25 (25%).
La incidencia es el número de casos nuevos que han ocurrido durante un intervalo de tiempo, dividido por el tamaño de la población en riesgo al comienzo del intervalo. Esta información es habitualmente obtenida de estudios de cohortes y expresada como proporción o tasa. Podemos diferenciar 2tipos de incidencias: la incidencia acumulada (proporción) y la densidad de incidencia (tasa).
La incidencia acumulada es una proporción que se calcula dividiendo el número de casos nuevos por la población en riesgo. Se utiliza cuando no se espera que la enfermedad se repita en un mismo sujeto y la población en riesgo sea estable. Por ejemplo, si en una población de 100.000 menores de 5 años se han diagnosticado en un año 20 meningitis, la incidencia acumulada es 0,0002 (o 2 por 10.000).
La densidad de incidencia es una tasa que se calcula dividiendo el número de casos nuevos por la suma de los periodos de tiempo que es seguida la población en riesgo (p. ej., meses o años). Se emplea cuando el riesgo de enfermedad es proporcional al tiempo de seguimiento, cada sujeto puede tener más de un caso y el tiempo de seguimiento de cada sujeto es diferente. Por ejemplo, si medimos la frecuencia de gastroenteritis en niños que acuden a una guardería en función del tiempo de permanencia en la misma y registramos 10 episodios nuevos de gastroenteritis (2 niños tuvieron más de un episodio) en una serie de 25 niños que asistieron a la guardería una media de 2 meses cada uno (50 meses en total), la densidad de incidencia de gastroenteritis sería de 0,2 casos (10/50) por cada niño y mes de exposición.
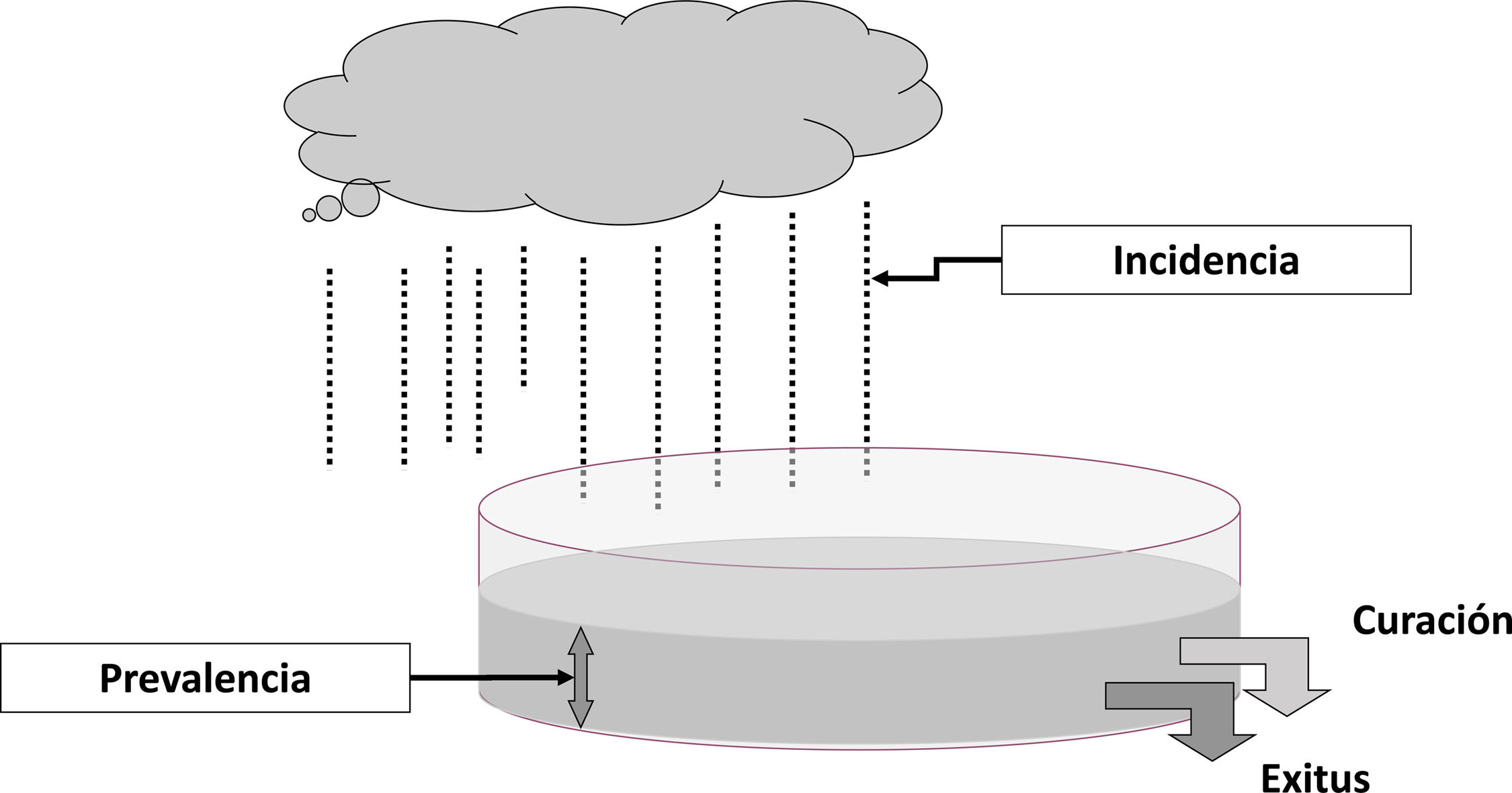
La prevalencia y la incidencia expresan información complementaria (fig. 1). Una enfermedad con alta incidencia, pero con alta mortalidad o alta curación tendrá una baja prevalencia en la población. Alternativamente, una enfermedad con una baja incidencia, pero con bajas mortalidad y curación (se cronifica) puede tener una alta prevalencia. El efecto de la mortalidad en la prevalencia puede repercutir en las características de las muestras seleccionadas para participar en un estudio, ya que la población susceptible de entrar en un estudio con casos prevalentes será una selección de pacientes con mejor pronóstico y menor presencia de factores de riesgo, que la población identificada en un estudio con casos incidentes.
Medidas de riesgo (asociación)En epidemiología el concepto de riesgo se entiende como la probabilidad de que los individuos expuestos a ciertos factores desarrollen en mayor o menor medida un resultado estudiado. En las tablas 1 y 2 se presentan las fórmulas de cálculo de las principales medidas de riesgo: el riesgo relativo (RR) y la odds ratio (OR).
El RR se calcula dividiendo la incidencia en el grupo de sujetos expuestos a un determinado factor de riesgo o protección entre la incidencia en el grupo no expuesto3. Solo puede ser calculado en estudios de seguimiento y mide la fuerza de la asociación entre exposición y enfermedad. Adopta valores entre 0 e infinito, menores de 1 para factores de protección (la incidencia es menor en los expuestos) y mayores de 1 para factores de riesgo (la incidencia es mayor en los expuestos); un RR de «1» supone el valor nulo (el riesgo en los 2grupos es igual), cuanto más se aleje el valor de 1, por arriba o por abajo, mayor será la fuerza de la asociación.
Cuando el seguimiento realizado a los sujetos incluidos en un estudio es heterogéneo, en vez de considerar la incidencia acumulada, para el cálculo de riesgos, se recurre a la densidad de incidencia, en la que cada sujeto es contabilizado en el denominador en función del tiempo que es seguido. En este caso el riesgo es estimado a partir de la razón de densidades de incidencia (RDI) entre grupos, que corresponde al cociente de las densidades de incidencia de los grupos expuesto y no expuesto.
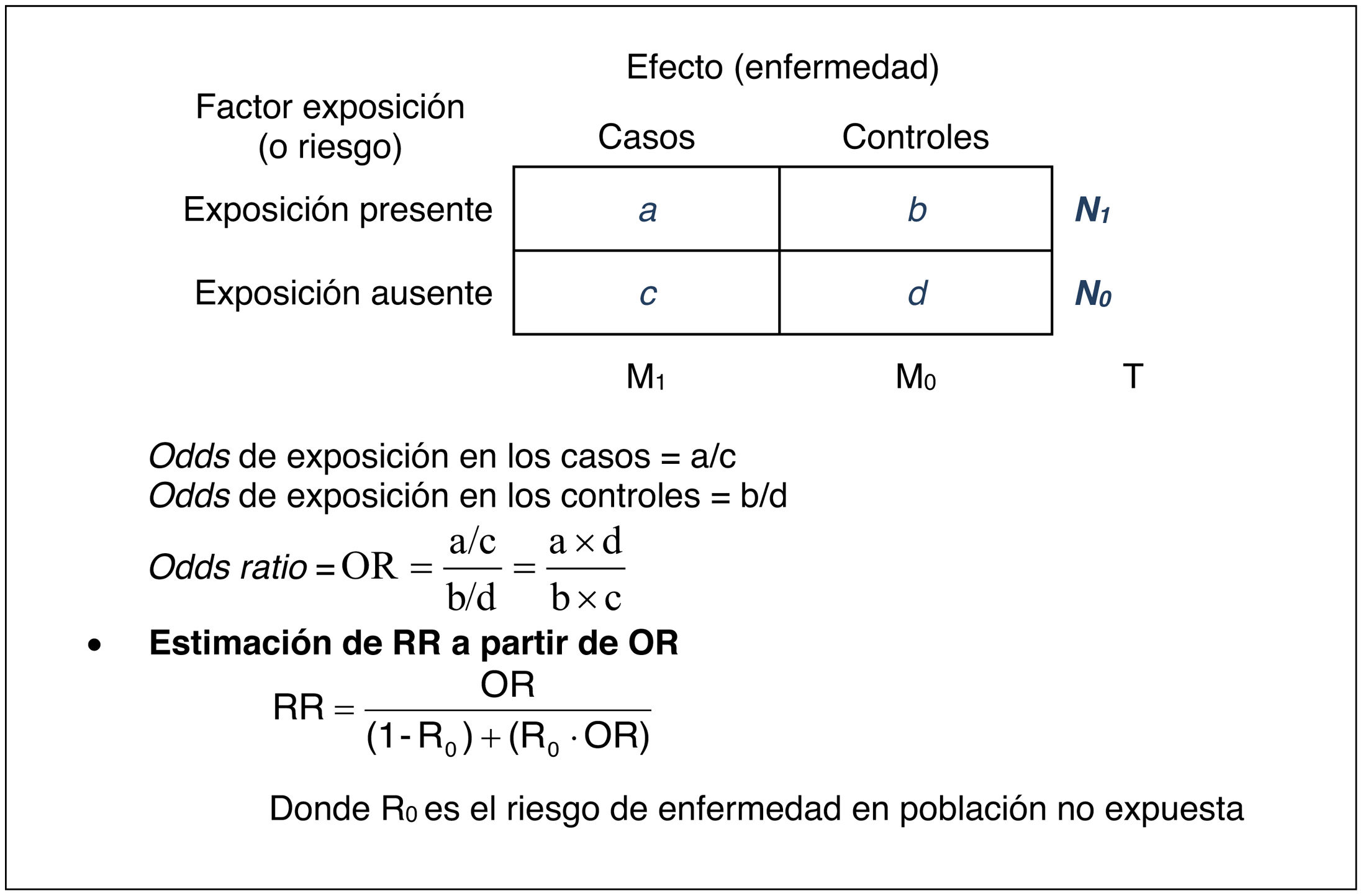
En los estudios sin seguimiento longitudinal (estudios de casos y controles), como no es posible calcular la incidencia, no puede calcularse el riesgo relativo4. Por ello, para estimar el riesgo se calcula la OR, que compara la odds de exposición (probabilidad de estar expuesto a un factor de riesgo dividida entre su complementario) en el grupo con enfermedad y la odds de exposición en el grupo control sin enfermedad, que se calcula dividiendo ambas odds. La interpretación de la OR es similar a la del RR; «1» supone el valor nulo, valores menores de 1 indican disminución del riesgo y mayores de 1 indican aumento del riesgo. Hay que tener en cuenta que solo cuando la enfermedad estudiada es muy poco frecuente el RR y la OR ofrecen valores similares.
Otra medida de riesgo empleada en estudios de supervivencia es el cociente de riesgos instantáneos, más conocida por su término en inglés: hazard ratio5. Se calcula en estudios de supervivencia (en los que la variable de efecto es el tiempo hasta que ocurre un evento) y refleja el cociente de riesgos condicionados en los grupos comparados a lo largo de todo el tiempo de seguimiento. La interpretación de la hazard ratio es similar a la del RR y la OR, el valor 1 indica ausencia de riesgo o asociación, valores mayores de 1, aumento del riesgo y, menores, disminución.
Medidas de impactoAunque con las medidas anteriores podemos estimar el riesgo que genera un factor de exposición sobre un efecto o enfermedad, esas medidas no nos informan del impacto que dicha exposición puede originar en el conjunto de casos existentes en una población. Esta información podemos extraerla de otras medidas, como la diferencia de riesgos o la proporción atribuible (tabla 1)3,6,7.
Ambas medidas son estimadoras del efecto absoluto que ejerce la exposición sobre la incidencia de un suceso en el grupo expuesto o en la población total. Se usan para evaluar la importancia clínica o sanitaria de una exposición y nos informan del porcentaje de incidencia que se reduciría si se eliminara el referido factor de exposición. Son, por consiguiente, muy útiles, tanto en la clínica como en salud pública, para cuantificar el posible impacto de diferentes medidas de intervención.
La diferencia de riesgos (DR) se calcula restando de la incidencia en el grupo expuesto al factor de riesgo, la incidencia en el grupo no expuesto. La DR es una medida de impacto absoluto, que adopta valores entre 0 y 1 (entre 0 y 100 si se expresa en tantos por ciento), constituyendo el «0» el valor nulo de ausencia de diferencias. La DR ofrece información independiente del riesgo relativo y puede variar, entre distintos grupos de pacientes, en función del riesgo propio de cada grupo. Así, podemos encontrarnos que factores que muestran un riesgo relativo muy alto apenas presenten modificaciones en la diferencia de riesgos porque el riesgo en la población (al margen de la contribución de dicho factor) sea muy bajo. Veamos un ejemplo: la incidencia de ingreso por bronquiolitis en un grupo de lactantes que acudían a guardería fue 0,02 (2%), mientras que la de los que eran cuidados en sus domicilios solo del 1%; el riesgo relativo indica un aumento de riesgo del 50% (RR 0,5), mientras que la diferencia de riesgos solo era del 1% (0,01).
La fracción o proporción atribuible en los expuestos (FAE), también conocida como riesgo atribuible, fracción etiológica, fracción atribuible o población de riesgo atribuible, se define como la proporción de casos nuevos de la enfermedad, en el grupo de sujetos expuestos, que son atribuibles al factor de riesgo de interés. Se calcula dividiendo la diferencia de riesgos, anteriormente calculada, entre la incidencia en el grupo expuesto. Una extensión de esta medida es la fracción o proporción atribuible poblacional (FAP), que extiende la proporción de casos nuevos a toda la población, esto es, al conjunto de sujetos tanto expuestos como no expuestos. Cuando el factor de riesgo es un factor de prevención, la medida de impacto estimada es la proporción evitable, que es la proporción de casos entre los expuestos, que se evitarían aplicando el factor de prevención. Estas medidas de impacto no pueden ser directamente estimadas con los datos de un estudio de casos y controles, ya que no nos ofrece estimaciones de incidencia. No obstante, podemos emplear la OR para estimarlas, como sustituto del RR, siempre que la enfermedad sea de baja prevalencia (en ese caso la OR se aproxima al RR; para enfermedades más frecuentes existen fórmulas de estimación del RR a partir de la OR).
Los resultados de los ensayos clínicos suelen reflejar el efecto beneficioso de intervenciones terapéuticas que reducen el riesgo en el grupo expuesto (tabla 3). Por ello, la diferencia de riesgos en este supuesto, conocida como reducción absoluta del riesgo (RAR), se calcula en sentido contrario, restando del riesgo en el grupo control el riesgo en el grupo de intervención. Si la RAR la dividimos por el riesgo en el grupo control, obtenemos la reducción relativa del riesgo (RRR) que expresa la proporción de riesgo evitado respecto del grupo control. Otra medida de impacto aplicable a estos estudios, de gran interés clínico, es el número necesario a tratar (NNT)8, que corresponde al inverso de la RAR (1/RAR), y que nos informa del número de pacientes que deberían ser tratados con la intervención terapéutica para que un caso se viera beneficiado, evitando un evento desfavorable.
Análisis de los ensayos clínicos
| Tasa de respuesta grupo de intervención. | Pi=nº eventos grupo intervencióntotal sujetos grupo intervención |
| Tasa de respuesta grupo control | Pc=nº eventos grupo controltotal sujetos grupo control |
| Reducción relativa del riesgo | RRR=Pc−PiPc |
| Reducción absoluta del riesgo | RAR=Pc−Pi |
| Número necesario a tratar | NNT=1RAR |
Existen otros números de impacto aplicables a estudios observacionales, no presentados aquí, que el lector interesado puede consultar en otras fuentes9,10.
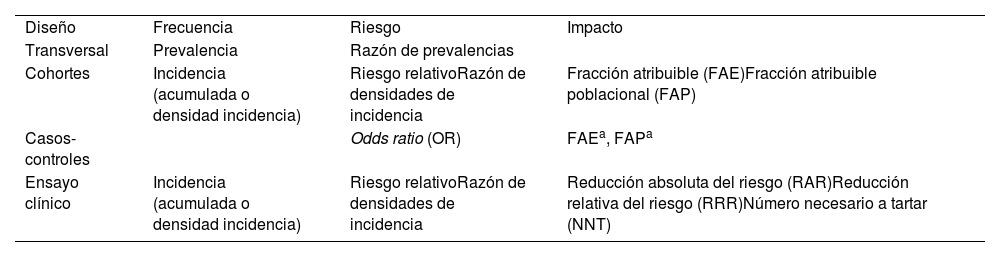
Elección de las medidas epidemiológicas en función del diseño del estudioEn la tabla 4 se presentan las medidas de frecuencia, riesgo e impacto más habituales en función del diseño del estudio, cuando el efecto se mide con una variable nominal dicotómica. Así, en un estudio transversal estimaremos la prevalencia; en un estudio de cohortes calcularemos la incidencia (acumulada o densidad de incidencia), el riesgo relativo (o la razón de densidades de incidencia) y las fracciones atribuibles (en expuestos y poblacional); en un estudio de casos y controles no podemos estimar medidas de frecuencia, pero sí de riesgo, la OR; finalmente, en un ensayo clínico calcularemos las incidencias, el riesgo relativo, las reducciones absoluta y relativa del riesgo y el número necesario a tratar.
Medidas de frecuencia, riesgo e impacto para variables nominales dicotómicas
| Diseño | Frecuencia | Riesgo | Impacto |
| Transversal | Prevalencia | Razón de prevalencias | |
| Cohortes | Incidencia (acumulada o densidad incidencia) | Riesgo relativoRazón de densidades de incidencia | Fracción atribuible (FAE)Fracción atribuible poblacional (FAP) |
| Casos-controles | Odds ratio (OR) | FAEa, FAPa | |
| Ensayo clínico | Incidencia (acumulada o densidad incidencia) | Riesgo relativoRazón de densidades de incidencia | Reducción absoluta del riesgo (RAR)Reducción relativa del riesgo (RRR)Número necesario a tartar (NNT) |
Cuando la medida de efecto de un estudio es una variable cuantitativa, la estimación de la diferencia de medias entre los grupos de estudio constituye en sí misma una medida de asociación e impacto (p. ej., diferencia de medias de hemoglobina glicosilada en 2grupos de diabéticos con pautas de insulina distintas).
En las figuras 2-4 se presentan los cálculos de medidas realizados con la calculadora disponible en línea Calcupedev11 de un estudio de cohortes, uno de casos y controles y un ensayo clínico. Basta con introducir los recuentos en la tabla de contingencia y el programa ofrece los cálculos de las medidas apropiadas con sus intervalos de confianza (IC) del 95%. Para entender los IC deberíamos explicar los fundamentos de la inferencia estadística, algo fuera del alcance de esta revisión12. Debemos tener en cuenta que cualquier estudio obtiene su información de una muestra de sujetos, que solo es una de las infinitas muestras posibles de una población; por ello, las medidas que estimemos serán solo una de las estimaciones posibles en dicha población. Para concretar la incertidumbre contamos con procedimientos estadísticos para estimar valores próximos a los obtenidos entre los que estaría el verdadero valor de la población. En concreto un IC del 95%, indica que hay una probabilidad del 95% de que el valor real de la población se sitúe entre los límites de dicho IC. Una interpretación más ortodoxa, dice que, si se extrajera un número infinito de muestras de la población para estimar el valor de interés, el 95% de sus IC del 95% contendrían el verdadero valor poblacional.
Con los datos del estudio de cohortes de la figura 2 podemos interpretar que el factor estudiado es un factor de riesgo (RR mayor de 1). Podemos decir que tenemos una confianza mayor del 95% de que el factor estudiado es realmente un factor de riesgo, porque el IC (1,065 a 3,755) no incluye en su interior el valor nulo para riesgos (el «1»). Además, podemos interpretar que el 50% del riesgo en los sujetos expuestos al factor de riesgo (FAE 0,50) y un 25% del riesgo en toda la población (FAP 0,25) es atribuible al factor de riesgo, aunque la estimación de la FAP es imprecisa, porque el IC del 95% incluye el valor nulo para proporciones (en este caso el «0»).
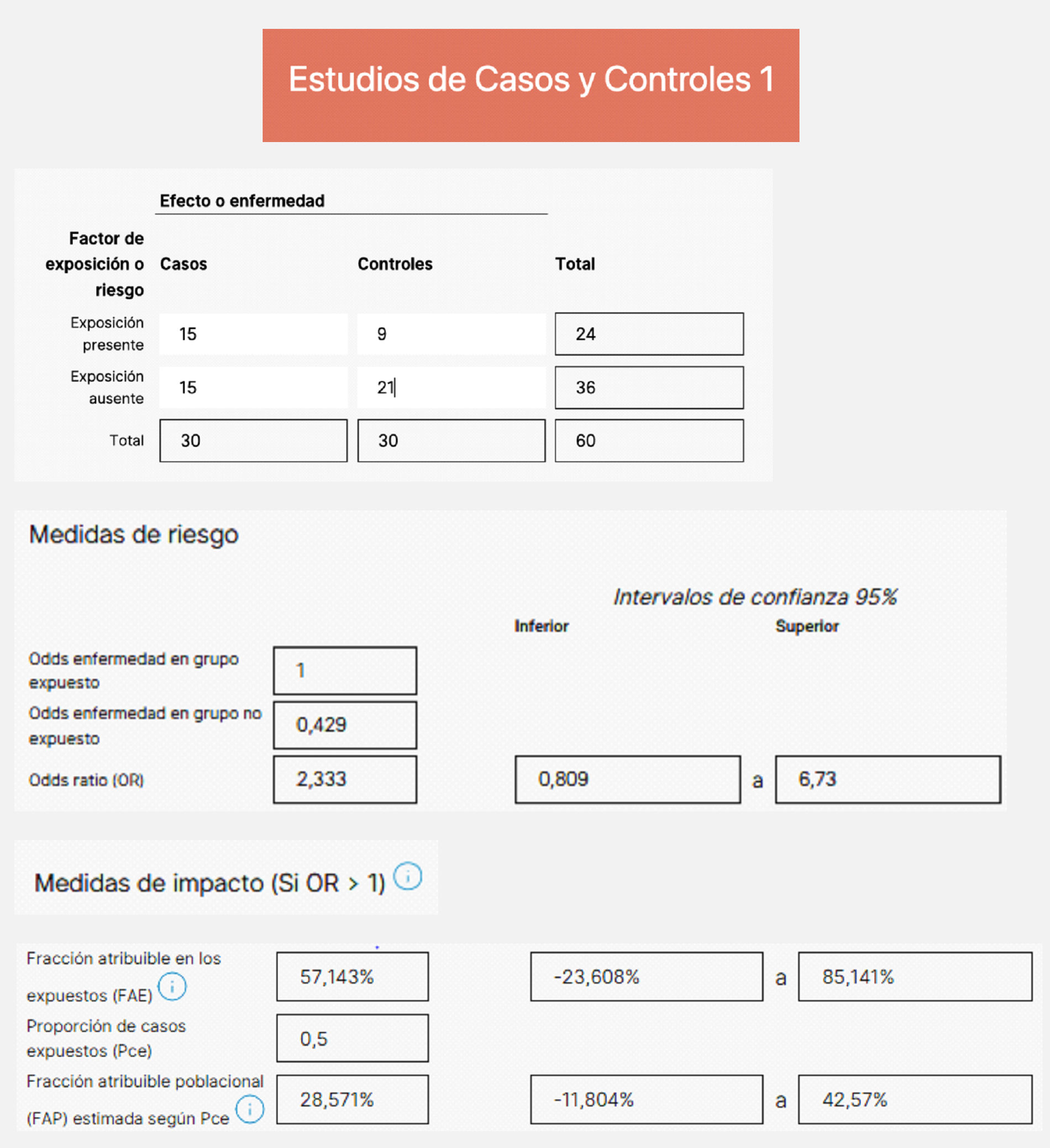
Con los datos del estudio de casos y controles de la figura 3 podemos interpretar que el factor de estudio podría ser un factor de riesgo (OR mayor que 1); sin embargo, observando el intervalo de confianza, que incluye en su interior el valor nulo para riesgos (el «1»), con la muestra estudiada no tenemos suficiente confianza para declararlo. Aunque la calculadora estima medidas de impacto, los cálculos se han hecho asumiendo que la OR equivale al RR, lo que no siempre es válido, dado que no conocemos las incidencias en la población expuesta y no expuesta (aquí solo sabemos el riesgo de exposición en los casos y controles no expuestos).
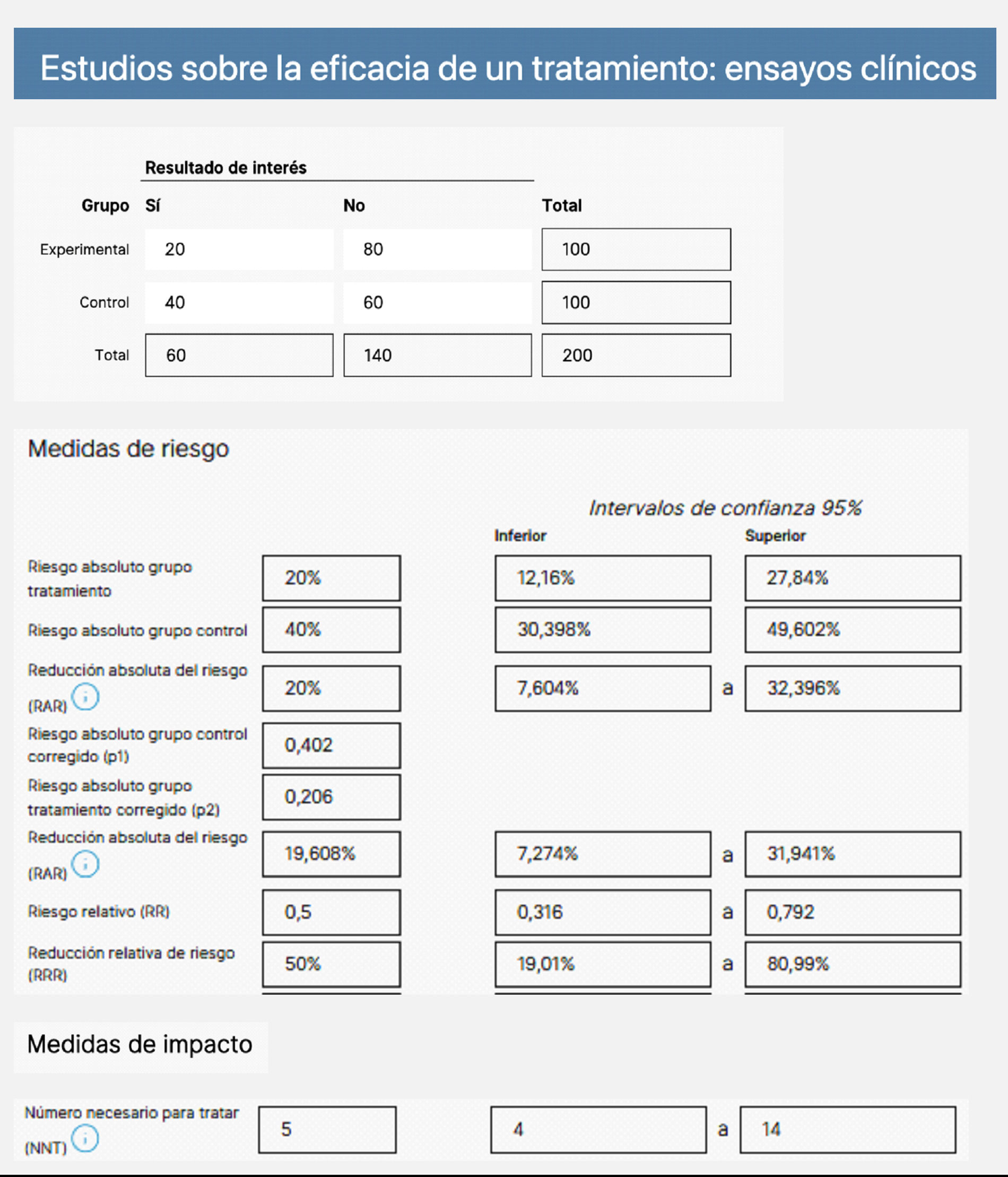
Con los datos del ensayo clínico de la figura 4 podemos interpretar que el tratamiento experimental reduce el riesgo del resultado de interés, con una reducción absoluta del riesgo del 20%. Vemos que el IC no incluye en su interior el valor nulo para diferencias de proporciones o medias (el «0»). Por ello tenemos una confianza mayor del 95% de que el tratamiento es eficaz. Además, podemos ver que en términos relativos el riesgo se reduce en un 50% con respecto al grupo control (reducción relativa del riesgo). Por último, el programa nos calcula el número necesario a tratar, pudiendo interpretar que tenemos que tratar a 5 pacientes con el tratamiento experimental para que mejore uno, con respecto al tratamiento control; el IC nos informa con una confianza del 95%, que en el mejor de los casos se beneficiaría uno de cada 4pacientes tratados y en el peor de los casos 14.
FinanciaciónLos autores declaran no tener ninguna subvención.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
María Salomé Albi Rodríguez, Pilar Aizpurua Galdeano, María Aparicio Rodrigo, Nieves Balado Insunza, Albert Balaguer Santamaría, Carolina Blanco Rodríguez, Jaime Javier Cuervo Valdés, M.ª Jesús Esparza Olcina, Sergio Flores Villar, Garazi Fraile Astorga, Javier González de Dios, Paz González Rodríguez, Rafael Martín Masot, M.ª Victoria Martínez Rubio, Begoña Pérez-Moneo Agapito, M.ª José Rivero Martín, Álvaro Gimeno Díaz de Atauri, Laura Cabrera Morente, Elena Pérez González, Juan Ruiz-Canela Cáceres.