En este trabajo se presenta unos nuevos métodos numéricos a partir de los índices metacarpofalángico y carpiano para el cálculo de la edad ósea, así como poder predecir la talla adulta por medio de ecuaciones multiregresión.
Material y métodosLa casuística longitudinal comprende a 160 niños zaragozanos sanos de ambos sexos, con edades comprendidas desde los 6meses hasta los 20años, estudiados anualmente, incluido el estudio radiológico. Para la labor estadística se ha utilizado el paquete estadístico «Statistix», así como el programa Excel.
ResultadosLos nuevos índices se encuentran íntimamente correlacionados con la edad cronológica, dando por ello lugar a ecuaciones predictivas para el cálculo de la edad ósea de niños hasta 20años, presentándose además ecuaciones propias hasta los cuatro, a efectos de poder afinar más el diagnóstico a estas cortas edades. Las edades óseas calculadas pueden ser llevadas tanto a tablas numéricas de desviación típica, como a una figura de equivalencias que nos dan el diagnóstico osificativo directamente. Las ecuaciones predictivas de talla adulta permiten una estimación fiable de la talla futura del niño a estudio. Estas estimaciones analizadas por el test de Student no han dado diferencias significativas respecto a la talla adulta que los niños de la casuística al final alcanzaron. Los resultados pueden obtenerse con una calculadora o a través de un programa informático a disposición gratuita del lector.
ConclusionesSon presentadas por vez primera, por métodos propios no foráneos, estándares de edad ósea, así como ecuaciones de predicción de talla adulta para el estudio de niños. Se invita al clínico a utilizar estos métodos metacarpofalángico y carpiano a fin de conseguir la experiencia necesaria para su idónea aplicación en población sana y con diversa patología.
This work presents new numerical methods from the meta-carpal-phalangeal and carpal indexes, for calculating bone age. In addition, these new methods enable the adult height to be predicted using multiple regression equations.
Materials and MethodsThe longitudinal case series studied included 160 healthy children from Zaragoza, of both genders, aged between 6months and 20years, and studied annually, including the radiological study. For the statistical analysis the statistical package “Statistix”, as well as the Excel program, was used.
ResultsThe new indexes are closely co-related to the chronological age, thus leading to predictive equations for the calculation of the bone age of children up to 20years of age. In addition, it presents particular equations for up to 4years of age, in order to optimise the diagnosis at these early ages. The resulting bones ages can be applied to numerical standard deviation tables, as well as to an equivalences chart, which directly gives us the ossification diagnosis. The predictive equations of adult height allow a reliable forecast of the future height of the studied child. These forecasts, analysed by the Student test did not show significant differences as regards the adult height that children of the case series finally achieved. The results can be obtained with a pocket calculator or through free software available for the reader.
ConclusionsFor the first time, and using a centre-developed and non-foreign methods, bones age standards and adult height predictive equations for the study of children, are presented. We invite the practitioner to use these meta-carpal-phalangeal and carpal methods in order to achieve the necessary experience to apply it to a healthy population and those with different disorders.
Los índices ebrí-metacarpofalángico (IMF) y carpiano (IC) son unos índices de valoración osificativo (IVO), hecho que permite llevar la edad ósea no solo a tablas numéricas estándar, sino a una figura de equivalencias que nos de directamente la edad ósea del niño. Estos índices están formados básicamente a partir de los máximos diámetros de los huesos carpianos, y metacarpofalángicos en los mismos dedos y huesos que los estudiados por Tanner II-Rus, aunque el IMF añade dos huesos más: las epífisis distales del cúbito y radio. El IC reúne sin embargo a diferencia de Tanner, 8 huesos del carpo, ya que incluye el psiforme, más las epífisis distales del cúbito y radio así como la epífisis del primer metacarpiano.
Históricamente fue Ebrí Torné el primer autor que utilizó el índice IMF en población suiza (estudio longitudinal de Zúrich) aplicándolo a dicha población. Realizó un estudio comparativo con la metódica de Tanner II Rus, demostrando la concordancia de ambos métodos además de encontrar una mayor simplicidad de su índice de valoración óseo metacarpofalángico respecto a la compleja metódica del autor inglés1.
El IC ya fue utilizado en población transversal española de 5.225 niños y longitudinal suiza2–7, pero dada la ausencia de datos longitudinales con estos métodos en población española, el objetivo de nuestro estudio ha sido el de aplicar este índice a la población aragonesa infantil procedente del estudio general «Andrea Prader», desarrollándose el estudio radiológico en el Hospital Miguel Servet de Zaragoza.
Este estudio somatométrico y radiológico «Andrea Prader» fue promovido por la Unidad de Endocrinología del citado hospital y autorizado por el Comité de Investigación, obteniéndose asimismo el consentimiento firmado por parte de los padres de los niños. Fue avalado y apoyado además por el Gobierno de Aragón8.
Aún sigue vigente hoy día la frase de Martí Henneberg de que la maduración ósea es el mejor indicador global de desarrollo biológico con que contamos en la especie humana9. La edad ósea (EO) expresa este proceso madurativo, requiriéndose estudios radiológicos sencillos para su determinación, siendo la radiografía de mano izquierda, en la opinión de la mayoría de los autores, la región anatómica preferida3,10.
Para el cálculo de la EO pueden utilizarse métodos morfológicos y numéricos. Nuestro método numérico presenta la ventaja sobre los morfológicos, de su mayor exactitud y de eliminar las asincronías y subjetividad del médico práctico a la hora de elegir la radiografía modelo en el atlas de Greulich-Pyle11.
Fue para solventar estas dificultades para lo que se crearon los métodos numéricos. El principal de ellos en la actualidad es el Tanner-Whitehouse. El autor inglés modificó algunos aspectos de su método publicado en 196212 y volvió a publicar en 1972 el denominado TW-Método II13. Presentó una escala por separado para los siete núcleos del carpo y los trece restantes de los huesos cortos y largos. A esta escala se la conoce con el nombre de Radius, Ulna, Short bones (RUS): Tanner II Rus, cuya fiabilidad es mayor que la TW2 carpal, con un mayor predictivo de la talla adulta, y una correlación mayor con los cambios puberales.
Andersen14 criticó el método I de Tanner, ya que observó que en los últimos estadios del carpo hay grandes saltos de puntuación, por lo que un estadio de diferencia puede suponer una dificultad manifiesta para reconocer los índices madurativos, debido a la superposición de los núcleos y a la no estricta universalidad de algunos de los índices descritos, por lo que además, un estadio de diferencia puede suponer una diferencia de edad ósea de 2años. El método II representó un gran avance pues su sistema de ponderación hace que la maduración ósea tenga expresión matemática, pero presenta el inconveniente de que la asignación de las etapas es también subjetiva, por lo que en la opinión de algunos autores15,16 la puntuación alcanzada no posee una exactitud absoluta.
Para solventar estas dificultades, es por lo que los autores ofrecen los índices IC e IMF, ya que la metodología básica de la que proceden es de fácil obtención, no requiere una gran experiencia técnica y minimiza las objeciones comentadas. Las medidas se realizan directamente en la radiografía, expresando éstas los máximos diámetros de los núcleos de osificación. Así y al ser recogidas todas las medidas en un índice promedio, se relativizan las asincronías y los propios defectos técnicos de medición, por otra parte insignificantes, ya que los núcleos son medidos con un calímetro, nonius en milímetros y sus décimas. Los dos dan lugar a ecuaciones predictivas de EO para niños hasta 20años, que se ofrecen como opciones no foráneas para calcular la maduración ósea. De parecida forma se comporta el llamado índice carpometacarpofalángico (ICMF) que valora no por separado sino conjuntamente ambas regiones anatómicas. Los tres aunque semejantes son distintos, y ofrecen resultados diferentes al clínico, siendo su utilización en la clínica la que definirá la idoneidad de uno u otros en el estudio del niño sano o con patología.
Con la creación de ecuaciones específicas para niños de hasta 4años, pretendemos ofrecer un diagnóstico de la EO más preciso para estas edades, sin la ligera sobrestimación que se produciría si utilizásemos las ecuaciones generales.
A través de los índices Ebrí, el clínico puede obtener también ecuaciones predictivas de talla adulta (PTA) que resultan operativas a partir de los 4años, siendo de fácil resolución, requiriéndose conocer únicamente la talla actual del niño a estudio, la talla media paterna y los propios índices. Estas PTA, como las propias de cálculo de la edad ósea, pueden utilizarse por separado o combinadas, siendo también la experiencia del clínico la que decidirá en un futuro la precisión de la PTA por uno u otros índices.
Material y métodosCasuísticaLa muestra total del estudio han sido 160 niños sanos (73 varones y 87 mujeres) que fueron medidos desde los 0,5 hasta los 20años inclusive. El número de individuos por edad y sexo que la componen viene detallado en la tablas 1 y 2.
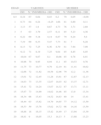
Índice metacarpofalángico. Media y± 1 desviación típica
| EDAD | VARONES | MUJERES | ||||||
| 1SD | N.° IND/MEDIA | -1SD | 1SD | N.° IND/MEDIA | - 1SD | |||
| 0,5 | 0,18 | 67 | 0,04 | 0,03 | 0,2 | 79 | 0,05 | −0,09 |
| 1 | 0,73 | 64 | 0,24 | −0,25 | 1,66 | 81 | 0,89 | 0,11 |
| 2 | 3,13 | 57 | 1,9 | 0,67 | 4,73 | 76 | 3,71 | 2,69 |
| 3 | 5 | 63 | 3,79 | 2,57 | 6,11 | 85 | 5,23 | 4,36 |
| 4 | 6,22 | 69 | 5,18 | 4,14 | 6,87 | 79 | 6,24 | 5,6 |
| 5 | 7,19 | 69 | 6,33 | 5,47 | 7,73 | 81 | 7 | 6,28 |
| 6 | 8,13 | 72 | 7,25 | 6,36 | 8,79 | 81 | 7,94 | 7,09 |
| 7 | 9,12 | 71 | 8,19 | 7,25 | 9,64 | 85 | 8,85 | 8,05 |
| 8 | 10,04 | 67 | 9,07 | 8,1 | 10,66 | 85 | 9,78 | 8,91 |
| 9 | 10,96 | 70 | 9,95 | 8,94 | 11,1 | 85 | 10,53 | 9,76 |
| 10 | 11,75 | 73 | 10,77 | 9,79 | 12,19 | 81 | 11,41 | 10,62 |
| 11 | 12,66 | 72 | 11,62 | 10,58 | 12,98 | 79 | 12,2 | 11,36 |
| 12 | 13,61 | 72 | 12,45 | 11,28 | 13,61 | 87 | 12,87 | 12,13 |
| 13 | 14,63 | 73 | 13,35 | 12,07 | 14,03 | 82 | 13,37 | 12,71 |
| 14 | 15,41 | 72 | 14,24 | 13,07 | 14,32 | 87 | 13,71 | 13,11 |
| 15 | 15,97 | 73 | 14,99 | 14,02 | 14,46 | 85 | 13,9 | 13,34 |
| 16 | 16,34 | 66 | 15,43 | 14,52 | 14,63 | 80 | 14 | 13,41 |
| 17 | 16,44 | 63 | 15,62 | 14,79 | 14,65 | 77 | 14,12 | 13,59 |
| 18 | 16,53 | 59 | 15,78 | 15,02 | 14,72 | 66 | 14,16 | 13,59 |
| 19 | 16,88 | 18 | 16,15 | 15,42 | 14,49 | 17 | 13,94 | 13,39 |
| 20 | 16,81 | 9 | 16,05 | 15,3 | 14,13 | 5 | 13,68 | 13,23 |
N.° IND:número de individuos.
Índice metacarpofalángico (IMF) valores en mm.
Edad en años.
Índice carpiano. Media y± 1 desviación típica
| EDAD | VARONES | MUJERES | ||||||
| 1Sd | N.° IND/MEDIAS | -1Sd | 1Sd | N.° IND/MEDIAS | -1Sd | |||
| 0,5 | 1,23 | 67 | 0,87 | 0,51 | 1,2 | 79 | 0,87 | 0,54 |
| 1 | 1,93 | 64 | 1,34 | 0,75 | 2,05 | 81 | 1,49 | 0,94 |
| 2 | 3,16 | 57 | 2,33 | 1,51 | 3,44 | 76 | 2,77 | 2,1 |
| 3 | 4,26 | 63 | 3,34 | 2,42 | 4,9 | 85 | 4,03 | 3,15 |
| 4 | 5,29 | 69 | 4,29 | 3,37 | 6,56 | 79 | 5,34 | 4,12 |
| 5 | 6,6 | 69 | 5,39 | 4,17 | 8,45 | 81 | 7 | 6,24 |
| 6 | 8,54 | 72 | 6,86 | 5,18 | 10,25 | 81 | 8,71 | 7,17 |
| 7 | 10,42 | 71 | 8,54 | 6,63 | 11,77 | 85 | 10,34 | 8,9 |
| 8 | 12,06 | 67 | 10,3 | 8,54 | 13,48 | 85 | 12,02 | 10,56 |
| 9 | 13,77 | 70 | 11,9 | 10,12 | 14,79 | 85 | 13,42 | 12,06 |
| 10 | 15,24 | 73 | 13,5 | 11,73 | 16,2 | 81 | 14,99 | 13,77 |
| 11 | 16,93 | 72 | 15,03 | 13,12 | 17,59 | 79 | 16,2 | 14,92 |
| 12 | 18,51 | 72 | 16,51 | 14,52 | 18,37 | 87 | 17,26 | 16,14 |
| 13 | 20,14 | 73 | 18,1 | 16,07 | 18,91 | 82 | 179 | 16,89 |
| 14 | 21,28 | 72 | 19,42 | 17,56 | 19,24 | 87 | 18,31 | 17,38 |
| 15 | 21,92 | 73 | 20,4 | 18,84 | 19,41 | 85 | 18,5 | 17,6 |
| 16 | 22,42 | 66 | 21,01 | 19,69 | 19,52 | 80 | 18,6 | 17,68 |
| 17 | 22,55 | 63 | 21,28 | 20,01 | 19,62 | 77 | 18,72 | 17,82 |
| 18 | 22,69 | 59 | 21,49 | 20,28 | 19,67 | 66 | 18,74 | 17,8 |
| 19 | 23,08 | 18 | 21,92 | 20,76 | 19,33 | 17 | 18,44 | 17,55 |
| 20 | 22,91 | 9 | 21,72 | 20,53 | 18,57 | 5 | 17,94 | 17,31 |
N.° IND=Número de individuos.
Índice carpiano (IC) en mm
Edad en años
Para este cometido, se empleó la encuesta de Graffar, 1956. De acuerdo a esta clasificación, se englobó a los participantes en categoría III, clase media-media; categoría IV, clase media-baja; categoría II, media-alta; categoría V, la más baja, y categoría I, la más alta.
Mediciones radiológicasCoincidiendo con la fecha del cumpleaños, los niños fueron radiografiados anualmente hasta los 20años, siendo distribuidos por grupos de estudio en intervalos anuales.
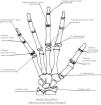
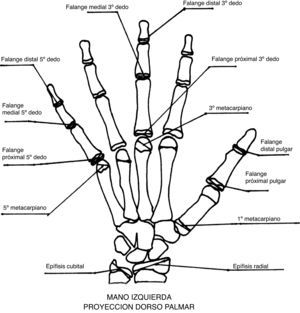
En nuestro estudio se procedió a la obtención del IMF, midiendo con un nonius las máximas distancias de los núcleos de osificación de los huesos metacarpianos y falanges: I, III, y V, así como de las epífisis distales cubital y radial en un total de 13 núcleos (fig. 1, radiografía anteroposterior de mano izquierda).
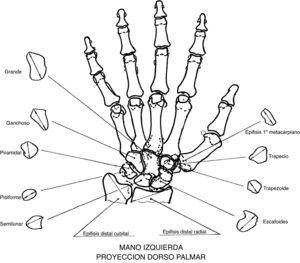
En el carpo para la obtención del IC, se procedió también con un nonius a la medición de las máximas distancias de los núcleos de osificación del carpo en radiografía anteroposterior de mano izquierda, comprendiendo las epífisis de radio, cúbito y epífisis del primer metacarpiano en un total de 11 núcleos de todos los niños en sus diferentes intervalos de edad (fig. 2).
Dichos índices expresados también en milímetros y son el resultado de la suma de los máximos diámetros de los núcleos citados, dividiéndose el sumando para simplificación numérica por 13 en el caso de IMF, y por 11 en el IC. En ambos casos, 13 y 11 son números fijos, estén presentes o no todos los núcleos en el momento de la medición. En las tablas 1 y 2, se ofrecen las medias y desviaciones típicas de IMF e IC en ambos sexos.
Todas las mediciones radiográficas del trabajo se realizaron por un único observador, y el estudio de repetibilidad practicado en 100 radiografías al mes de su primera medición fue superior al 95%.
Análisis estadísticoPara la labor estadística, se ha utilizado el paquete estadístico «Statistix», software versión 9, año 2000, así como el programa Excel para la confección de las tablas que presentamos. Se ha efectuado una estadística descriptiva (medias y desviación estándar), así como coeficientes de correlación de las variables estudiadas. De igual forma para el IMF e IC, se han confeccionado ecuaciones para el cálculo de la EO a partir de ambos índices, basadas en la ecuación de la recta de regresión, dada su excelente correlación con la edad cronológica. Estas ecuaciones permiten al resolverlas darnos por ambos las edades óseas (EO) del niño, pudiendo ser llevadas estas a tablas de referencia que muestran la media y desviación típica de EO en ambos sexos (tablas 3 y 4). Como se ha comentado ya, presentamos dos tipos de ecuaciones, unas para el estudio general de niños hasta 20años, y otras específicas para niños hasta 4años, debido a la frecuente existencia de asincronías de los núcleos de osificación en las primeras edades infantiles que dificultan el diagnóstico de una precisa edad ósea para estas edades. De esta forma se obtiene una mejora diagnóstica para todas las edades.
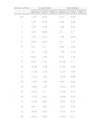
Media y una desviación típica de la edad ósea metacarpofalángica
| EDAD AÑOS | VARONES | MUJERES | ||
| MEDIAS | DESV. TÍPICA | MEDIAS | DESV. TÍPICA | |
| 0,5 | 0,25 | 0,13 | 0,83 | 0,16 |
| 1 | 0,45 | 0,5 | 1,8 | 0,89 |
| 2 | 1,45 | 1,26 | 2,39 | 1,16 |
| 3 | 3,39 | 1,24 | 4,15 | 1 |
| 4 | 4,83 | 1,06 | 5,3 | 0,73 |
| 5 | 6 | 0,88 | 6,18 | 0,82 |
| 6 | 6,95 | 0,9 | 7,26 | 0,97 |
| 7 | 7,92 | 0,96 | 8,29 | 0,91 |
| 8 | 8,82 | 1 | 9,37 | 1 |
| 9 | 9,73 | 1,03 | 10,23 | 0,88 |
| 10 | 10,57 | 1,01 | 11,24 | 0,9 |
| 11 | 11,45 | 1,06 | 12,14 | 0,95 |
| 12 | 12,3 | 1,19 | 12,92 | 0,85 |
| 13 | 13,23 | 1,31 | 13,5 | 0,76 |
| 14 | 14,14 | 1,19 | 13,89 | 0,69 |
| 15 | 14,92 | 1 | 14,1 | 0,64 |
| 16 | 15,37 | 0,93 | 14,22 | 0,67 |
| 17 | 15,56 | 0,84 | 14,37 | 0,6 |
| 18 | 15,73 | 0,78 | 14,4 | 0,64 |
| 19 | 16,11 | 0,75 | 14,15 | 0,62 |
| 20 | 16,01 | 0,77 | 13,85 | 0,51 |
Edad ósea en años.
Media y una desviación típica de la edad ósea carpiana
| EDAD AÑOS | VARONES | MUJERES | ||
| MEDIAS | DESV.TÍPICA | MEDIAS | DESV.TÍPICA | |
| 0,5 | 1,29 | 0,25 | 0,15 | 0,26 |
| 1 | 1,63 | 0,42 | 0,66 | 0,44 |
| 2 | 2,35 | 0,59 | 1,69 | 0,54 |
| 3 | 3,07 | 0,66 | 2,7 | 0,7 |
| 4 | 3,75 | 0,71 | 3,76 | 0,98 |
| 5 | 4,54 | 0,87 | 5,1 | 1,17 |
| 6 | 5,6 | 1,2 | 6,48 | 1,24 |
| 7 | 6,8 | 1,35 | 7,79 | 1,15 |
| 8 | 8,07 | 1,26 | 9,15 | 1,18 |
| 9 | 9,25 | 1,31 | 10,28 | 1,1 |
| 10 | 10,36 | 1,26 | 11,55 | 0,98 |
| 11 | 11,46 | 1,36 | 12,56 | 1,06 |
| 12 | 12,53 | 1,43 | 13,38 | 0,89 |
| 13 | 13,67 | 1,46 | 13,9 | 0,81 |
| 14 | 14,62 | 1,33 | 14,22 | 0,74 |
| 15 | 15,31 | 1,1 | 14,38 | 0,73 |
| 16 | 15,76 | 0,97 | 14,46 | 0,74 |
| 17 | 15,95 | 0,91 | 14,57 | 0,72 |
| 18 | 16,1 | 0,87 | 14,57 | 0,75 |
| 19 | 16,41 | 0,83 | 14,33 | 0,71 |
| 20 | 16,27 | 0,85 | 13,92 | 0,5 |
Edad ósea en años.
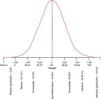
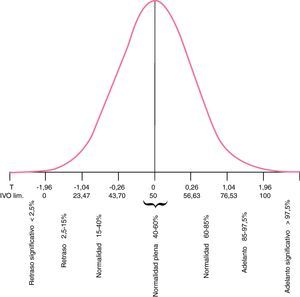
Con los (IVO)-IMF e IC que aportamos obtenidos a partir del IMF e IC, se consigue una optimización de la lectura del proceso osificativo del niño a estudio. Los resultados obtenidos, cuyos valores en ambos sexos oscilan entre 0 y 100, comprenden±1,96SD, es decir, el 95% de los niños cuya osificación es normal, siendo conveniente investigar aquellos niños que presenten valores negativos de IVO inferior a 0 o superiores a 100 (-1,96 a 1,96 desviación típica), ya que su edad ósea podría estar retrasada o adelantada significativamente. Estos IVO pueden ser llevados también a una figura de equivalencias respecto a la edad ósea, donde se lee el diagnóstico osificativo directo del niño: normal, retraso normal, adelanto normal, o retraso/adelanto significativo (fig. 3).
Se han creado también ecuaciones de PTA en ambos sexos, utilizando estos índices: IMF e IC, añadidos a la talla actual del niño a estudio (ecuaciones de dos variables) (tablas 5-8), como de tres variables añadiendo a las anteriores la talla media paterna (tablas 9-12).
Ecuaciones de predicción de talla adulta a partir de dos variables: IMF, y talla de los niños, por grupos de edad. Varones
| G | ÍNDICES | N.° | a | b1 | b2 | p |
| 4 | IMF | 68 | 28,94 | −0,42 | 1,43 | p<0,001 |
| 5 | IMF | 69 | 38,46 | −0,44 | 1,26 | p<0,001 |
| 6 | IMF | 72 | 37,67 | −1,01 | 1,24 | p<0,001 |
| 7 | IMF | 71 | 42,8 | −0,97 | 1,14 | p<0,001 |
| 8 | IMF | 66 | 40,94 | −0,33 | 1,07 | p<0,001 |
| 9 | IMF | 70 | 41,75 | −0,76 | 1,05 | p<0,001 |
| 10 | IMF | 72 | 46,52 | −1,42 | 1,03 | p<0,001 |
| 11 | IMF | 72 | 56,27 | −1,58 | 0,95 | p<0,001 |
| 12 | IMF | 71 | 68,28 | −2,14 | 0,89 | p<0,001 |
| 13 | IMF | 72 | 79,44 | −3,01 | 0,87 | p<0,001 |
| 14 | IMF | 72 | 83,8 | −3,2 | 0,84 | p<0,001 |
| 15 | IMF | 72 | 69,43 | −2,93 | 0,89 | p<0,001 |
| 16 | IMF | 66 | 50,01 | −0,96 | 0,81 | p<0,001 |
| 17 | IMF | 63 | 15,55 | −0,71 | 0,98 | p<0,001 |
| 18 | IMF | 57 | 28,55 | 1,97 | 0,66 | p<0,001 |
| 19 | IMF | 18 | 3,88 | −0,26 | 1 | p<0,001 |
| 20 | IMF | 9 | 0 | 0 | 1 | p<0,001 |
Correlaciones múltiples por grupos de edades: y=a+b1.x1+b2.x2.
y=talla adulta G =grupos de edad
x1=índice IMF
x2=talla a la edad
N°=número de individuos
p=significatividad
Coeficientes de regresión: b1,b2
Ordenada en el origen: a.
Ecuaciones de predicción de talla adulta a partir de dos variables: IMF, y talla de los niños, por grupos de edad. Mujeres
| G | ÍNDICES | N.° | a | b1 | b2 | p |
| 4 | IMF | 79 | 34,66 | −1,48 | 1,33 | p<0,001 |
| 5 | IMF | 81 | 50,67 | −0,8 | 1,07 | p<0,001 |
| 6 | IMF | 80 | 138,04 | 1,68 | 0,09 | p<0,001 |
| 7 | IMF | 85 | 33,75 | −2,39 | 1,23 | p<0,001 |
| 8 | IMF | 85 | 79,84 | −0,18 | 0,66 | p<0,001 |
| 9 | IMF | 85 | 37,4 | −2,48 | 1,13 | p<0,001 |
| 10 | IMF | 81 | 82,41 | −1,59 | 0,7 | p<0,001 |
| 11 | IMF | 79 | 72,94 | −2,61 | 0,84 | p<0,001 |
| 12 | IMF | 87 | 70,79 | −1,97 | 0,77 | p<0,001 |
| 13 | IMF | 82 | 30,45 | −1,77 | 0,99 | p<0,001 |
| 14 | IMF | 87 | −1,77 | −0,81 | 1,1 | p<0,001 |
| 15 | IMF | 85 | −2,35 | −0,39 | 1,05 | p<0,001 |
| 16 | IMF | 79 | 1,34 | −0,45 | 1,03 | p<0,001 |
| 17 | IMF | 74 | −0,16 | −0,21 | 1,02 | p<0,001 |
| 18 | IMF | 64 | 1,9 | −0,05 | 0,99 | p<0,001 |
| 19 | IMF | 17 | 1,44 | 0,1 | 0,98 | p<0,001 |
| 20 | IMF | 5 | 0 | 0 | 1 | p<0,001 |
Correlaciones múltiples por grupos de edades: y=a+b1.x1+b2.x2.
y=talla adulta G =grupos de edad
x1=índice IMF
x2=talla a la edad
N.°=número de individuos
p=significatividad
Coeficientes de regresión: b1,b2
Ordenada en el origen: a.
Ecuaciones para predicción de talla adulta a partir de dos variables: IC y talla de los niños, por grupos de edad. Varones
| G | ÍNDICES | N.° | a | b1 | b2 | p |
| 4 | IC | 68 | 29,33 | −0,26 | 1,4 1 | p<0,001 |
| 5 | IC | 69 | 40,45 | 0,02 | 1,22 | p<0,001 |
| 6 | IC | 72 | 37,33 | −0,35 | 1,2 | p<0,001 |
| 7 | IC | 71 | 42,42 | −0,3 | 1,1 | p<0,001 |
| 8 | IC | 66 | 38,45 | −0,27 | 1,09 | p<0,001 |
| 9 | IC | 70 | 37,67 | −0,53 | 1,08 | p<0,001 |
| 10 | IC | 72 | 41,29 | −0,85 | 1,04 | p<0,001 |
| 11 | IC | 72 | 48,3 | −1,04 | 0,99 | p<0,001 |
| 12 | IC | 71 | 62,03 | −1,16 | 0,89 | p<0,001 |
| 13 | IC | 72 | 76,9 | −1,63 | 0,82 | p<0,001 |
| 14 | IC | 72 | 79,72 | −1,54 | 0,77 | p<0,001 |
| 15 | IC | 72 | 61,62 | −1,71 | 0,88 | p<0,001 |
| 16 | IC | 66 | 48,34 | −0,3 | 0,77 | p<0,001 |
| 17 | IC | 63 | 13,17 | −0,46 | 0,98 | p<0,001 |
| 18 | IC | 57 | 34,24 | 1,33 | 0,64 | p<0,001 |
| 19 | IC | 18 | 3,23 | −0,07 | 0,99 | p<0,001 |
| 20 | IC | 9 | 0 | 0 | 1 | p<0,001 |
Correlaciones múltiples por grupos de edades: y=a+b1.x1+b2.x2.
y=talla adulta G =grupos de edad en años
x1=índice IC
x2=talla a la edad
N.°=número de individuos
p=significatividad
Coeficientes de regresión:b1, b2
Ordenada en el origen: a.
Ecuaciones para predicción de talla adulta a partir de dos variables: IC y talla de los niños, por grupos de edad. Mujeres
| G | ÍNDICES | N.° | a | b1 | b2 | p |
| 4 | IC | 79 | 34,23 | −0,7 | 1,28 | p<0,001 |
| 5 | IC | 81 | 40,51 | −0,91 | 1,17 | p<0,001 |
| 6 | IC | 80 | 144,73 | 0,64 | 0,1 | p<0,001 |
| 7 | IC | 85 | 27,47 | −1,39 | 1,22 | p<0,001 |
| 8 | IC | 85 | 78,76 | −0,3 | 0,68 | p<0,001 |
| 9 | IC | 85 | 30,22 | −1,65 | 1,16 | p<0,001 |
| 10 | IC | 81 | 79,49 | −1,32 | 0,74 | p<0,001 |
| 11 | IC | 79 | 68,44 | −1,74 | 0,84 | p<0,001 |
| 12 | IC | 87 | 71,29 | −0,78 | 0,69 | p<0,001 |
| 13 | IC | 82 | 27,93 | −0,22 | 0,88 | p<0,001 |
| 14 | IC | 87 | −5,4 | −0,02 | 1,05 | p<0,001 |
| 15 | IC | 85 | −5,45 | 0,12 | 1,02 | p<0,001 |
| 16 | IC | 79 | −0,7 | 0,07 | 1 | p<0,001 |
| 17 | IC | 75 | −1,04 | 0 | 1 | p<0,001 |
| 18 | IC | 64 | 1,46 | 0,01 | 0,99 | p<0,001 |
| 19 | IC | 17 | 1,54 | 0,03 | 0,98 | p<0,001 |
| 20 | IC | 5 | 0 | 0 | 1 | p<0,001 |
Correlaciones múltiples por grupos de edades: y=a+b1.x1+b2.x2.
y=talla adulta G =grupos de edad en años
x1=índice IC
x2=talla a la edad
N.°=número de individuos
p=significatividad
Coeficientes de regresión:b1, b2.
Ordenada en el origen: a.
Ecuaciones de predicción de talla adulta a partir de tres variables: IMF, talla de los niños y talla media paterna por grupos de edad. Varones
| G | ÍNDICES | N.° | a | b1 | b2 | b3 | p |
| 4 | IMF | 68 | 1,74 | −0,29 | 1,14 | 0,34 | p<0,001 |
| 5 | IMF | 69 | 6,8 | −0,38 | 1,02 | 0,35 | p<0,001 |
| 6 | IMF | 72 | 2,67 | −1 | 1,02 | 0,36 | p<0,001 |
| 7 | IMF | 71 | 1,45 | −1,09 | 0,94 | 0,41 | p<0,001 |
| 8 | IMF | 66 | 8,84 | −0,7 | 0,92 | 0,33 | p<0,001 |
| 9 | IMF | 70 | 15,56 | −1 | 0,93 | 0,27 | p<0,001 |
| 10 | IMF | 72 | 15,59 | −1,65 | 0,9 | 0,31 | p<0,001 |
| 11 | IMF | 72 | 14,62 | −1,91 | 0,82 | 0,39 | p<0,001 |
| 12 | IMF | 71 | 21,45 | −2,11 | 0,73 | 0,43 | p<0,001 |
| 13 | IMF | 72 | 22,4 | −2,67 | 0,69 | 0,49 | p<0,001 |
| 14 | IMF | 72 | 33,16 | −2,53 | 0,66 | 0,43 | p<0,001 |
| 15 | IMF | 72 | 29,36 | −2,41 | 0,73 | 0,35 | p<0,001 |
| 16 | IMF | 66 | 12,62 | −0,81 | 0,65 | 0,39 | p<0,001 |
| 17 | IMF | 63 | 4,81 | −0,71 | 0,93 | 0,11 | p<0,001 |
| 18 | IMF | 57 | 15,27 | 1,78 | 0,59 | 0,17 | p<0,001 |
| 19 | IMF | 18 | 5,4 | −0,27 | 1,01 | −0,02 | p<0,001 |
| 20 | IMF | 9 | 0 | 0 | 1 | 0 | p<0,001 |
Correlaciones múltiples por grupos de edades: y=a+b1.x1+b2.x2+b3.x3.
G =grupos de edad
y=talla adulta
x1=índice IMF
x2=talla a la edad
x3=talla media paterna
N.°=número de individuos
p=significatividad
Coeficientes de regresión:b1,b2,b3
Ordenada en el origen: a
Ecuaciones de predicción de talla adulta a partir de tres variables: IMF, talla de los niños y talla media paterna por grupos de edad. Mujeres
| G | ÍNDICES | N.° | a | b1 | b2 | b3 | p |
| 4 | IMF | 79 | 3,69 | −1,52 | 1,21 | 0,26 | p<0,001 |
| 5 | IMF | 81 | 12,02 | −1 | 0,98 | 0,3 | p<0,001 |
| 6 | IMF | 80 | 59,86 | 1,22 | 0,08 | 0,51 | p<0,001 |
| 7 | IMF | 85 | 9,4 | −2,17 | 1,11 | 0,22 | p<0,001 |
| 8 | IMF | 85 | 44,99 | −0,17 | 0,55 | 0,29 | p<0,001 |
| 9 | IMF | 85 | 17,02 | −2,33 | 1,04 | 0,18 | p<0,001 |
| 10 | IMF | 81 | 45,94 | −1,38 | 0,59 | 0,3 | p<0,001 |
| 11 | IMF | 79 | 32,23 | −2,41 | 0,73 | 0,32 | p<0,001 |
| 12 | IMF | 87 | 33,3 | −1,65 | 0,65 | 0,31 | p<0,001 |
| 13 | IMF | 82 | 9,57 | −1,76 | 0,92 | 0,19 | p<0,001 |
| 14 | IMF | 87 | −3,1 | −0,81 | 1,09 | 0,01 | p<0,001 |
| 15 | IMF | 85 | 0,83 | −0,4 | 1,07 | −0,03 | p<0,001 |
| 16 | IMF | 79 | 3,82 | −0,47 | 1,04 | −0,02 | p<0,001 |
| 17 | IMF | 74 | 3,03 | −0,2 | 1,03 | −0,03 | p<0,001 |
| 18 | IMF | 64 | 3,06 | −0,05 | 0,99 | 0 | p<0,001 |
| 19 | IMF | 17 | 2,21 | 0,1 | 0,98 | 0 | p<0,001 |
| 20 | IMF | 5 | 0 | 0 | 1 | 0 | p<0,001 |
Correlaciones múltiples por grupos de edades: y=a+b1.x1+b2.x2+b3.x3.
G =grupos de edad
y=talla adulta
x1=índice IMF
x2=talla a la edad
x3=talla media paterna
N.°=número de individuos
p=significación
Coeficientes de regresión:b1,b2,b3.
Ordenada en el origen: a.
Ecuaciones para predicción de talla adulta a partir de tres variables: IC, talla de los niños y talla media paterna por grupos de edad. Varones
| G | ÍNDICES | N.° | a | b1 | b2 | b3 | p |
| 4 | IC | 68 | −0,45 | −0,36 | 1,15 | 0,35 | p<0,001 |
| 5 | IC | 69 | 6,1 | −0,16 | 1,01 | 0,35 | p<0,001 |
| 6 | IC | 72 | 1,82 | −0,37 | 0,99 | 0,36 | p<0,001 |
| 7 | IC | 71 | 0,19 | −0,39 | 0,9 | 0,41 | p<0,001 |
| 8 | IC | 66 | 5,94 | −0,43 | 0,93 | 0,33 | p<0,001 |
| 9 | IC | 70 | 10,76 | −0,65 | 0,95 | 0,27 | p<0,001 |
| 10 | IC | 72 | 10,45 | −0,96 | 0,91 | 0,31 | p<0,001 |
| 11 | IC | 72 | 6,13 | −1,19 | 0,85 | 0,39 | p<0,001 |
| 12 | IC | 71 | 10,36 | −1,28 | 0,74 | 0,45 | p<0,001 |
| 13 | IC | 72 | 15,22 | −1,57 | 0,66 | 0,51 | p<0,001 |
| 14 | IC | 72 | 23,3 | −1,31 | 0,6 | 0,48 | p<0,001 |
| 15 | IC | 72 | 18,49 | −1,51 | 0,73 | 0,39 | p<0,001 |
| 16 | IC | 66 | 10,07 | −0,4 | 0,62 | 0,4 | p<0,001 |
| 17 | IC | 63 | 2,46 | −0,46 | 0,93 | 0,11 | p<0,001 |
| 18 | IC | 57 | 19,09 | 1,23 | 0,57 | 0,18 | p<0,001 |
| 19 | IC | 18 | 4,6 | −0,06 | 1 | −0,02 | p<0,001 |
| 20 | IC | 9 | 0 | 0 | 1 | 0 | p<0,001 |
Correlaciones múltiples por grupos de edades: y=a+b1.x1+b2.x2+b3.x3.
G =Grupos de Edad en años
y=talla adulta
x1=índice IC
x2=talla a la edad
x3=talla media paterna
N.°=número de individuos
p=significación
Coeficientes de regresión: b1, b2, b3.
Ordenada en el origen: a.
Ecuaciones de predicción de talla adulta a partir de tres variables: IC, talla de los niños y talla media paterna por grupos de edad. Mujeres
| G | ÍNDICES | N.° | a | b1 | b2 | b3 | p |
| 4 | IC | 79 | 5,92 | −0,63 | 1,15 | 0,25 | p<0,001 |
| 5 | IC | 81 | 7,18 | −0,85 | 1,05 | 0,27 | p<0,001 |
| 6 | IC | 80 | 60,92 | 0,51 | 0,08 | 0,53 | p<0,001 |
| 7 | IC | 85 | 7,67 | −1,23 | 1,11 | 0,19 | p<0,001 |
| 8 | IC | 85 | 44,46 | −0,26 | 0,57 | 0,29 | p<0,001 |
| 9 | IC | 85 | 12,14 | −1,56 | 1,07 | 0,17 | p<0,001 |
| 10 | IC | 81 | 43,12 | −1,23 | 0,63 | 0,3 | p<0,001 |
| 11 | IC | 79 | 30,23 | −1,56 | 0,73 | 0,31 | p<0,001 |
| 12 | IC | 87 | 31,61 | −0,69 | 0,58 | 0,32 | p<0,001 |
| 13 | IC | 82 | 6,81 | −0,25 | 0,81 | 0,2 | p<0,001 |
| 14 | IC | 87 | −7,26 | −0,02 | 1,04 | 0,01 | p<0,001 |
| 15 | IC | 85 | −2,82 | 0,11 | 1,04 | −0,02 | p<0,001 |
| 16 | IC | 79 | 0,99 | 0,07 | 1 | −0,01 | p<0,001 |
| 17 | IC | 75 | 2,27 | −0,01 | 1,02 | −0,03 | p<0,001 |
| 18 | IC | 64 | 2,56 | 0 | 0,99 | 0 | p<0,001 |
| 19 | IC | 17 | 2,19 | 0,02 | 0,99 | 0 | p<0,001 |
| 20 | IC | 5 | 0 | 0 | 1 | 0 | p<0,001 |
Correlaciones múltiples por grupos de edades: y=a+b1.x1+b2.x2+b3.x3.
G =grupos de edad en años
y=talla adulta
x1=índice IC
x2=talla a la edad
x3=talla media paterna
N.°=número de individuos
p=significación
Coeficientes de regresión:b1, b2, b3.
Ordenada en el origen: a.
La mayoría de la población zaragozana pertenece a la categoría socioeconómica III y IV, con un total de 90,1%. Estos resultados son representativos de la mayoría de la población general zaragozana.
En la tablas 1 y 2, se ofrecen por sexos y edades la media y una desviación típica de los índices IMF e IC, lo cual nos da ya una orientación acerca del estado osificativo del niño.
A partir de los índices IMF o IC y como resultado de sus correlación estadística con la edad cronológica (a medida que aumenta la edad cronológica, aumentan los índices y viceversa) hemos obtenido en ambos sexos ecuaciones de predicción de la EO expresándose éstas en años.
Los coeficientes de correlación (r) de IMF han sido de 0,96 en varones en un total de 1.305 correlaciones, y de 0,93 en mujeres en un total de 1.556 correlaciones, con una significatividad estadística de p<0,001. Los r de IC respecto a la edad cronológicahan sido de 0,96 en varones en un total de 1.306 correlaciones y de 0,95 en mujeres en un total de 1.557 correlaciones, con una significatividad estadística en ambos sexos de p<0,001. Las EO que se pueden estimar con ambos índices oscilan desde los 0,5 hasta los 20años.
A partir de la ecuación de la recta de regresión de estas correlaciones, es de donde se obtienen las ecuaciones para el cálculo de la EO. Derivadas de estas correlaciones estadísticas y a efectos de simplificación matemática, ofrecemos estas ecuaciones finales listas para ser utilizadas por el clínico. Así en este ejemplo de ecuación: (y=a+b.x), y es igual a la edad ósea a calcular, a es la ordenada en el origen que se suma al resultado de multiplicar b, que es el coeficiente de regresión por x, que es IMF o IC. El resultado de la ecuación nos da la EO del niño a estudio, ya sea a través de un índice u otro. Seguidamente estas EO, obtenidas en años, pueden ser contrastadas sus valores con tablas específicas de medias y desviaciones típicas de EO (tablas 3 y 4 en ambos sexos).
Ofrecemos a continuación y en ambos sexos las ecuaciones modelo a resolver, para obtener las EO ya por IMF o IC. Se presentan las ecuaciones generales de niños hasta 20años y específicas para niños de 0,5 a 4años. Estas últimas correlaciones de niños hasta 4años también han sido significativas a p<0,001 por los dos índices.
Ecuación general de los varones hasta los 20años: Edad ósea=-0,504+1,029xIMF
Y en las mujeres hasta los 20años: Edad ósea=-1,869+1,149xIMF
Ecuación general de los varones hasta los 20años: Edad ósea=-0,670+0,718xIC
En mujeres hasta los 20años: Edad ósea=-0,548+0,807xIC
Ecuaciones de los varones de 0,5 a 2años. Edad ósea=0, 8251+0,4342xIMF
Varones de 0,5 a 4años. Edad ósea=0,8789+0,5361xIMF
Mujeres de 0,5 a 2años. Edad ósea=0,6498+0,3267xIMF
Mujeres de 0,5 a 4años. Edad ósea=0,5657+0,4744xIMF
Varones de 0,5 a 2años. Edad ósea=0, 398+0,49203xIC
Varones de 0,5 a 4años. Edad ósea=0,28649+0,76369xIC
Mujeres de 0,5 a 2años. Edad ósea=0,22601+0,53048xIC
Mujeres de 0,5 a 4años. Edad ósea=0,22582+0,64250xIC
A efectos de ofrecer al clínico un diagnóstico más preciso del proceso osificativo del niño a estudio, y siguiendo a Ebrí Torné2,17 se ha procedido a obtener los llamados: IVO de IMF e IC.
Para obtener el IVO hay que llevar a las ecuaciones que presentamos seguidamente los IMF o IC con valores expresados en mm, así como las edades cronológicas (EC) del niño expresadas en años. El cálculo puede obtenerse con una sencilla calculadora, al efectuar distintas sumas, restas y multiplicaciones. Puede utilizarse también para ello un programa informático a disposición gratuita del lector que nos da directamente los IVO por sus diferentes tres índices, al introducir los datos de las medidas de los huesos carpianos y metacarpofalángicos. Los resultados se llevan a la figura de equivalencias de la EO (fig. 3).
Así para los varones hasta 20años, este IVO-IMF es=41,3+17,8xIMF-17,3xEC
Para las mujeres hasta los 20años, el IVO-IMF es=24,8+15,5xIMF-13,5xEC
Varones hasta 20años, el IVO-IC es=62, 3+13, 2xIC-18, 4xEC
Mujeres hasta 20años, el IVO-IC es=41, 7+12,2xIC-15,1xEC
De igual forma que para las edades óseas, hemos obtenido las ecuaciones de los IVO-IMF e IC de varones y mujeres de 0,5 a 2años y de 0,5 a 4años.
Así, IVO-IMF. Varones de 0,5 a 2años es=100,919+26,796xIMF-61,711xEC
Varones 0,5-4años. IVO-IMF=93,049+26,259xIMF-48,978xEC
Y para las mujeres de 0,5-2años. IVO-IMF=112,492+31,419xIMF-96,167 xEC
Mujeres de 0,5-4años. IVO-IMF=85,244+29,554xIMF-62,294xEC
Varones de 0,5 a 2años. IVO-IC=73,772+29,388xIC-59,729xEC
Varones de 0,5-4años. IVO-IC=60,619+28,306xIC-37,065xEC
Mujeres de 0,5-2años. IVO-IC=67,131+40,210xIC-75,799xEC
Mujeres de 0,5-4años. IVO-IC=60,623+30,225xIC-47,042 xEC
En las tablas 5 a 12, se ofrecen las ecuaciones de regresión en ambos sexos, tanto de dos como de tres variables, y a través del IMF e IC, para obtener las PTA de los niños a estudio.
La resolución de estas ecuaciones es sencilla ya que a pie de tabla se detallan las significaciones de las variables analizadas. El cálculo puede realizarse con el uso de calculadora o empleando el programa informático. Así como ejemplo, en la ecuación básica de tres variables: y=a+b1.x1+b2.x2+b3.x3; y es la talla adulta a calcular, a (ordenada en el origen) posee un valor diferente para cada grupo de edad, que se suma al producto de multiplicar b1 (coeficiente de regresión), cuyo valor se encuentra en la tabla en cada grupo de edad por x1 (IMF o IC) calculado en el niño en cuestión. El valor obtenido a su vez se suma al producto de multiplicar b2 (coeficiente de regresión detallado en cada grupo de edad en la tabla) por x2 (talla del niño que hemos medido). El valor obtenido vuelve a sumarse al producto de multiplicar b3 (coeficiente de regresión cuyo valor se detalla en cada grupo de edad en la tabla) por x3 (talla media paterna), dándonos el resultado final que es la talla adulta.
DiscusiónLa valoración de la edad ósea se utiliza frecuentemente en patología endocrinológica de la nutrición y del crecimiento, además de servir de base para los modernos métodos de predicción de talla adulta, así como para poder comprobar la respuesta al tratamiento de aquellas patologías que pueden acelerarla o endentecerla. Así mismo, resulta interesante en el terreno antropológico, deportivo escolar, así como para el control de niños adoptados por instituciones18. De igual forma, y con repetidas valoraciones de las predicciones de talla adulta, se puede seguir controlando la respuesta terapéutica en determinadas endocrinopatías19–22.
Con las ecuaciones de predicción de EO que aportamos al clínico a partir de los dos índices, éste dispone de dos herramientas eficaces para el diagnóstico de la EO de niños a estudio. Con la figura de equivalencias del IVO a EO, podemos afinar aún más el diagnóstico. Las tablas de medias y desviación típica de IMF y de EO completan el estudio para obtener la valoración osificativa del niño que presentamos al pediatra para que lo utilice en su práctica diaria. Así mismo, éste puede obtener la PTA a través de las ecuaciones predictivas que se ofrecen.
Como ya se ha comentado el método de Tanner experimentó duras críticas por diversos autores14, y aunque su método II resultó un gran avance al poder el método expresarse de forma matemática, en la opinión de algunos autores15,16 la puntuación alcanzada no posee una exactitud absoluta.
Para solventar las críticas a este método, ya Ebrí Torné introdujo un método numérico propio aplicado al carpo en población española mixta transversal de 5.225 individuos hasta los 17 años, que ofrecía según este autor una mayor objetividad para el cálculo de la edad ósea2–6,23. Así mismo, aplicó su método específicamente a población infantil de recién nacidos españoles hasta 2 y 4años24.
El método de Greulich tampoco ha escapado a las críticas de Tanner que hemos hecho alusión. Recordemos como los estudios realizados en poblaciones normales muestran un retraso en relación a los valores que da el atlas, que puede ser de hasta 1año. Ésto es debido a que los niños del atlas eran maduradores precoces. Un dato muy a tener en cuenta es que existe una disociación entre la maduración de los huesos del carpo y el resto de los huesos de la mano, que puede ser hasta de 2años o más, y es aconsejable por ello dar un valor para el carpo y otro para el resto, tomando como edad ósea a la media aritmética de ambos. Hasta una desviación de 1año entre la edad cronológica y la edad ósea se acepta como normal a ciertas edades, comenzando ya aparte de los 1,5años en los varones y 3años en las niñas25. Con frecuencia además ocurre que un núcleo de osificación difiere mucho en relación a los del resto de la mano. Marti Henneberg9,26 también comentó a este respecto cómo Greulich y Pyle utilizan en primer lugar como unidad de medida la edad cronológica, escondiendo este hecho que la maduración ósea tiene un ritmo propio que se acelera en determinadas edades como la pubertad, no siendo todos los años de maduración iguales. No es igual tampoco la maduración puberal que la maduración en la primera infancia; además el ritmo de maduración difiere en diversos niños, al producirse la aceleración de la pubertad en diversas edades y por ello los clasifica en maduradores normales, precoces o tardíos. El atlas de Greulich y Pyle nos ofrece además únicamente el promedio, pero no el margen de normalidad expresado en percentiles o desviaciones estándar, dentro del cual una radiografía no se puede considerar patológica. El atlas, afirmaba también Martí-Henenberg, nos sumerge en una visión estática que los métodos numéricos han hecho evolucionar. No obstante a este respecto, Ebrí Torné en 1988 publicó un atlas radiográfico de carpo y tarso2 seleccionó la «imagen promedio modelo» del índice carpiano y tarsiano de cada intervalo de edad, creando una secuencia fotográfica de un teórico niño ideal, como si fueran un niño y niña real desde el nacimiento hasta los 16años en el tarso y 17 en el carpo. Un año más tarde que este autor comparase su metódica respecto a los mismos huesos estudiados por TWII-Rus1 realizó también en la misma población suiza de 10 a 22años un estudio comparativo de las edades óseas de estos niños por diferentes métodos: Tanner-carpal, Tanner-Rus, Ebrí carpal, ebrí-metacarpofalángico y Greulich y Pyle27. Comprobó su concordancia aun existiendo diferencias estadísticamente significativas entre ellas, de manera que cada una se comportaba de forma metodológicamente diferente según su propia originalidad. Así mismo evidenció como la metodología Ebrí salvaba las asincronías del Greulich-Pyle y los grandes saltos de puntuación en los estadios del carpo que asigna Tanner, así como la dificultad que apuntaba Andersen, para reconocer los indicadores de madurez en los últimos estadios.
La aplicación del IVO-IMF e IVO-IC en población longitudinal aragonesa suple la carencia de estudios de la edad ósea en nuestro país con métodos no foráneos. Además, hay que tener en cuenta que la maduración ósea al estar influenciada por diferentes factores: genéticos, ambientales, socioeconómicos.., es por lo que se recomienda al investigador la creación de estándares propios para cada población, a efectos de no utilizar estándares foráneos en nuestros niños que exigen una corrección de la EO, siendo éste uno de nuestros objetivos al crear esta serie. El potencial de ésta se revelará a medida que sea utilizado, así como sus posibles limitaciones, aunque creemos están relativizadas respecto a las presentadas por otros autores. Por estas razones es por lo que presentamos también en este trabajo ecuaciones específicas para edades de los niños por debajo de los 4años para afinar el diagnostico óseo.
Dada la importancia que tiene hoy día, especialmente para el pediatra y padres de familia, como ya comentaron Sobradillo et al28 el poder conocer la talla futura de los niños, hemos aportado a este estudio ecuaciones de PTA. A este respecto, y con esta misma metódica pero aplicada a población suiza, Ebrí Torné en 1997 publicó en una casuística longitudinal desde los 10 hasta los 22años su método de PTA, pero desarrollado en esta ocasión a partir de la edad ósea metacarpofalángica29. Este mismo autor estableció un estudio comparativo de las PTA en población suiza entre diferentes métodos (índice metacarpofalángico, Bayley-Pinneau y Tanner II) donde se valoraron todas las predicciones por el método de Student, así como sus errores absolutos y relativos. Se encontraron menos errores por el método de predicción IMF, mientras Bayley-Pinneau tendía a dar estimaciones más altas sobre todo en los varones, y Tanner subestimaba las predicciones en ambos sexos30.
Respecto a la metódica PTA a través del IC, recordemos como antecedentes históricos a Ebrí Torné, que en 1995 publicó unas ecuaciones de PTA para niño español basadas en este índice y en las mismas variables actuales, procedentes de 836 niños españoles, cuyos datos de talla adulta se obtuvieron al cabo de los años de realizar el estudio primigenio de 1980. Estos niños ya adultos procedían del estudio general de 5.225 niños realizado por el autor y publicado en 19882. Las ecuaciones de regresión de estos 836 niños ya adultos se agruparon por grupos de edades desde los 4 hasta los 18años31. Comprobó este autor también que existía también una correlación estadísticamente significativa entre el número de pie adulto y la talla adulta. Destacó entonces el interés de seguir realizando estudios longitudinales de maduración ósea y de predicción de talla adulta con sus métodos en futuras series como las realizadas en la actualidad.
Un año antes, Ebrí Torné había publicado un nuevo método para PTA, basado en la EO carpiana, aplicado en población longitudinal suiza desde los 10 hasta los 18años. Empleó ecuaciones multiregresión confeccionadas a partir de EO carpales y tallas obtenidas en el momento de efectuar el estudio radiológico, además de constantes de talla y de EO32.
En este trabajo, las ecuaciones de PTA, expuestas en Resultados, se ofrecen al pediatra en dos y tres variables, de tal forma que las PTA pueden obtenerse con y sin la talla media paterna. Las predicciones de estos niños aragoneses respecto a la talla adulta conocida no dan diferencias estadísticamente significativas, hecho que avala la validez de estas ecuaciones para ser utilizadas por el clínico.
Creemos que nuestro estudio, desarrollado en niño zaragozano, dada su diversidad étnica, puede aplicarse también a niño español, tanto respecto al cálculo de la EO como para la PTA.
Se infiere la utilidad de aplicar esta metódica predictiva de EO y PTA a nuevas series prospectivas de estudio a efectos de ir creando diversos estándares poblacionales.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Agradecemos al Doctor Ferrández Longás (Servicio de Pediatría del Hospital Miguel Servet) su inestimable colaboración por la aportación de las radiografías de los niños, actualmente adultos que han servido de base al Estudio Longitudinal de niño aragonés (Centro Andrea Prader).